Đề bài
Cho tứ diện \(SABC\). Trên \(SA\), \(SB\) và \(SC\) lần lượt lấy các điểm \(D\), \(E\) và \(F\) sao cho \(DE\) cắt \(AB\) tại \(I\), \(EF\) cắt \(BC\) tại \(J\), \(FD\) cắt \(CA\) tại \(K\). Chứng minh ba điểm \(I, J, K\) thẳng hàng.
Phương pháp giải - Xem chi tiết
Để chứng minh ba điểm thẳng hàng ta chứng minh ba điểm đó cùng thuộc hai mặt phẳng phân biệt.
Lời giải chi tiết
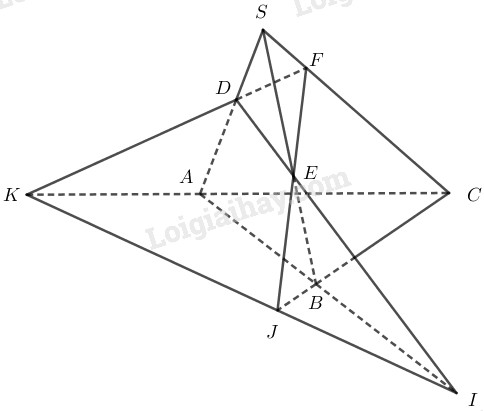
Ta có: \(I = DE \cap AB\)
Mà \(DE \subset (DEF) \Rightarrow I \in (DEF)\)
và \(AB \subset (ABC) \Rightarrow I \in (ABC)\)
Suy ra \(I\in (DEF)\cap (ABC)\)
Ta có: \(J = EF \cap BC\)
Mà \(EF \subset (DEF) \Rightarrow J \in (DEF)\)
và \(BC \subset (ABC) \Rightarrow J \in (ABC)\)
Suy ra \(J\in (DEF)\cap (ABC)\)
Tương tự, \(K\in (DEF)\cap (ABC)\) nên \(I\), \(J\), \(K\) thuộc giao tuyến của \((ABC)\) và \((DEF)\) nên \(I\), \(J\), \(K\) thẳng hàng.
soanvan.me
