Đề bài
Cho hình chóp \(S.ABCD\). \(M\) và \(N\) tương ứng là các điểm thuộc các cạnh \(SC\) và \(BC\). Tìm giao điểm của đường thẳng \(SD\) với mặt phẳng \((AMN)\).
Phương pháp giải - Xem chi tiết
Cách tìm giao điểm đường thẳng \(d\) với mặt phẳng \((P)\) trong bài là:
- Tìm mặt phẳng \((Q)\) sao cho \(d\subset (Q)\).
- Tìm \(d’\) là giao tuyến của \((P)\) và \((Q)\).
- Giao điểm cần tìm chính là giao điểm của \(d\) và \(d’\).
Trong bài ta có \(SD\subset (SBD)\) như vậy mục tiêu là tìm \(d’=(AMN)\cap(SBD)\). Giao điểm cần tìm là giao của \(SD\) và \(d’\).
Lời giải chi tiết
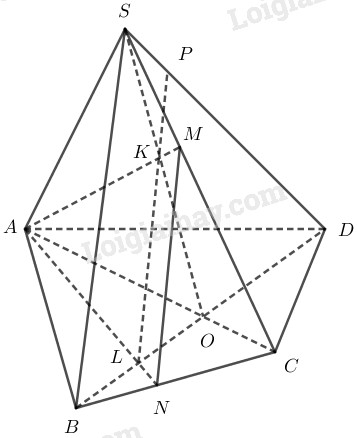
Gọi \(O = AC \cap BD\)
Trong \((SAC)\) gọi \(K = SO \cap AM\)
Trong \((ABCD)\) gọi \(L = BD \cap AN\)
Khi đó \(KL=(SBD)\cap(AMN)\)
Suy ra \(SD\cap (AMN)=SD\cap KL=P\)
Ta có \(P \in KL,KL \subset (AMN) \)
\(\Rightarrow P \in (AMN)\) và \(P \in SD\)
\(\Rightarrow P = (AMN) \cap SD\).
soanvan.me
