Đề bài
Cho tam giác \(ABC\) cân tại \(A,\) các đường phân giác \(BE,\) \(CF.\) Chứng minh rằng \(BFEC\) là hình thang cân có đáy nhỏ bằng cạnh bên.
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Hình thang là tứ giác có hai cạnh đối song song.
+) Hình thâng cân là hình thang có hai góc kề một đáy bằng nhau.
Lời giải chi tiết
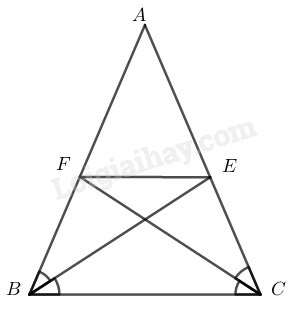
+) \(∆ ABC\) cân tại \(A\) nên \(AB = AC\) và \(\widehat B=\widehat C\)
+) Do BE và CF lần lượt là tia phân giác của góc B và góc C nên ta có:
\(\widehat {ABE} =\displaystyle {{\widehat B} \over 2}\) và \(\displaystyle \widehat {ACF}= {{\widehat C} \over 2} \)
Suy ra \(\widehat {ABE}=\displaystyle {{\widehat B} \over 2} = {{\widehat C} \over 2} = \widehat {ACF}\)
Xét hai tam giác \(AEB\) và \(AFC\) có:
\(\widehat A\) là góc chung
\(AB = AC\) (chứng minh trên)
\(\widehat {ABE} = \widehat {ACF}\) (chứng minh trên)
\( \Rightarrow \Delta AEB = \Delta AFC\left( {g.c.g} \right)\)
\( \Rightarrow AE = AF \Rightarrow \Delta AEF\) cân tại \(A\)
\( \Rightarrow \widehat {AFE} =\displaystyle {{{{180}^0} - \widehat A} \over 2}\)
Trong tam giác \(\Delta ABC\) cân tại A có: \(\,\,\widehat B = \displaystyle {{{{180}^0} - \widehat A} \over 2}\)
\( \Rightarrow \widehat {AFE} = \widehat B\), mà hai góc ở vị trí đồng vị nên \( FE//BC\)
\(\Rightarrow\) tứ giác \(BFEC\) là hình thang.
Ta có: \(\widehat B=\widehat C\) (tam giác \(ABC\) là tam giác cân tại \(A\))
\(\Rightarrow\) hình thang \(BFEC\) là hình thang cân.
Vì \(FE//BC\) \(\Rightarrow \widehat {FEB}=\widehat {CBE}\) (hai góc so le trong)
Mà \(\widehat {CBE}=\widehat {FBE}\) (\(BE\) là phân giác góc \(B\))
\(\Rightarrow \widehat {FBE}=\widehat {FEB}\)
\(\Rightarrow \Delta BFE\) là tam giác cân tại \(F\)
\(\Rightarrow EF=BF\)
Vậy hình thang BFEC là hình thang cân có đáy nhỏ bằng cạnh bên.
soanvan.me
