Đề bài
Hình thang cân \(ABCD\) có đáy nhỏ \(AB\) bằng cạnh bên \(AD.\) Chứng minh rằng \(CA\) là tia phân giác của góc \(C.\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Trong hình thang cân, hai cạnh bên bằng nhau.
Lời giải chi tiết
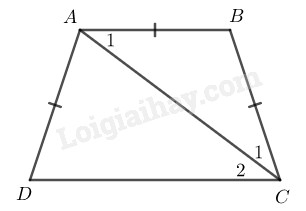
Ta có:
\(AB = AD \;\;\;(gt)\)
\(AD = BC\) (tính chất hình thang cân)
\(⇒ AB = BC\) do đó \(∆ ABC\) cân tại \(B\)
\(\Rightarrow {\widehat A_1} = {\widehat C_1}\) (1) (tính chất tam giác cân)
Mặt khác, ABCD là hình thang có đáy là AB nên \(AB // CD\;\;\; \)
Suy ra \({\widehat A_1} = {\widehat C_2}\) (2) (hai góc so le trong)
Từ (1) và (2) suy ra \({\widehat C_1} = {\widehat C_2}\) (cùng bằng \(\widehat A_1)\)
Vậy \(CA\) là tia phân giác của \(\widehat {BCD}\).
soanvan.me
