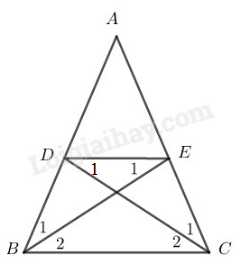
Cho tam giác \(ABC\) cân tại \(A.\) Lấy điểm \(D\) trên cạnh \(AB,\) điểm \(E\) trên cạnh \(AC\) sao cho \(AD = AE.\)
LG a
\(\) Tứ giác \(BDEC\) là hình gì \(?\) Vì sao \(?\)
Phương pháp giải:
Ta sử dụng kiến thức:
+) Hình thang là tứ giác có hai cạnh đối song song.
+) Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
Lời giải chi tiết:
Ta có: \(AD = AE \;\;\; (gt)\)
\(⇒ ∆ ADE\) cân tại \(A\)
\( \Rightarrow \widehat {ADE} = \displaystyle {{{{180}^0} - \widehat A} \over 2}\)
\(∆ ABC\) cân tại \(A\)
\( \Rightarrow \widehat {ABC} = \displaystyle {{{{180}^0} - \widehat A} \over 2}\)
Suy ra: \(\widehat {ADE} = \widehat {ABC}\)
\(⇒ DE // BC\) (vì có cặp góc đồng vị bằng nhau)
Tứ giác \(BDEC\) là hình thang
\(\widehat {ABC} = \widehat {ACB}\) (tính chất tam giác cân)
Hay \(\widehat {DBC} = \widehat {ECB}\). Vậy BDEC là hình thang cân
LG b
\(\) Các điểm \(D,\) \(E\) ở vị trí nào thì \(BD = DE = EC\) \(?\)
Phương pháp giải:
Ta sử dụng kiến thức:
+) Hình thang là tứ giác có hai cạnh đối song song.
+) Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
Lời giải chi tiết:
\(\) Giả sử: \(BD = DE\) \(⇒ ∆ BDE\) cân tại \(D\)
\( \Rightarrow {\widehat B_1} = {\widehat E_1}\)
Mà \({\widehat E_1} = {\widehat B_2}\) (so le trong)
\( \Rightarrow {\widehat B_1} = {\widehat B_2}\)
\(\Rightarrow BE\) là tia phân giác của \(\widehat {ABC}.\)
Giả sử: \(DE = EC\) \(⇒∆ DEC\) cân tại \(E\)
\( \Rightarrow {\widehat D_1} = {\widehat C_1}\)
\({\widehat D_1} = {\widehat C_2}\) (so le trong)
\( \Rightarrow {\widehat C_1} = {\widehat C_2}\)
\(\Rightarrow CD\) là tia phân giác của \(\widehat {ACB}.\)
Vậy khi \(BE\) là tia phân giác của \(\widehat {ABC}\), \(CD\) là tia phân giác của \(\widehat {ACB}\) thì \(BD = DE = EC.\)
soanvan.me