Đề bài
Hình thang cân \(ABCD\) có đường chéo \(DB\) vuông góc với cạnh bên \(BC,\) \(DB\) là tia phân giác của góc \(D.\) Tính chu vi của hình thang, biết \(BC = 3cm.\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Trong hình thang cân, hai cạnh bên bằng nhau.
+) Trong tam giác vuông, hai góc nhọn phụ nhau.
+) Trong hình thang cân, hai góc kề một đáy bằng nhau.
+) Tam giác có đường phân giác là đường cao thì đó là tam giác cân.
+) Tam giác cân có một góc \(60^0\) là tam giác đều.
Lời giải chi tiết
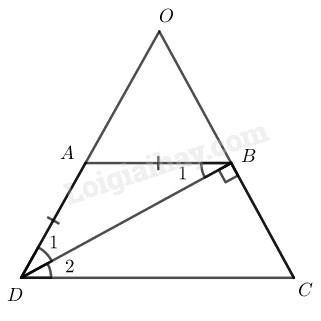
Vì ABCD là hình thang cân nên \(AD = BC = 3 \;\;(cm)\) (tính chất hình thang cân)
Ta có: \(AB//CD\) (do ABCD là hình thang) nên \(\widehat {ABD} = \widehat {BDC}\) (so le trong)
Lại có DB là tia phân giác của góc ADC nên:
\(\eqalign{
& \widehat {ADB} = \widehat {BDC} \cr
& \Rightarrow \widehat {ABD} = \widehat {ADB} \cr} \)
\(⇒ ∆ ABD\) cân tại \(A\)
\(⇒ AB = AD = 3\;\; (cm)\)
\(∆ BDC\) vuông tại \(B\)
\( \Rightarrow \widehat {BDC} + \widehat C = {90^0}\) (tổng 2 góc nhọn trong tam giác vuông bằng \(90^0)\)
Mà \(\widehat {ADC} = \widehat C\) (do ABCD là hình thang cân), \(\widehat {BDC} = \displaystyle {1 \over 2}\widehat {ADC}\) (do DB là phân giác góc D) nên \(\widehat {BDC} = \displaystyle {1 \over 2}\widehat C\)
\(\Rightarrow \widehat C + \displaystyle {1 \over 2}\widehat C = {90^0} \Rightarrow \dfrac{3}2\widehat C = {90^0}\Rightarrow \widehat C = {60^0}\)
Gọi \(O\) là giao điểm của của \(AD\) và \(BC\).
Do \( \Delta ODC\) có \(DB\) vừa là phân giác, vừa là đường cao nên \( \Delta ODC\) là tam giác cân tại \(D.\)
Ta lại có: \( \widehat C=60^0\) nên \( \Delta ODC\) là tam giác đều.
\(\Rightarrow CD=OC=2BC=2.3=6\;\; (cm)\)
Chu vi hình thang \(ABCD\) bằng:
\(AB + BC + CD + DA \)\(= 3+3 +6 +3=15 \;\;\;(cm)\)
soanvan.me
