Đề bài
Tam giác \(ABC\) có đáy \(BC\) cố định và dài \(4\,cm.\) Đỉnh \(A\) di chuyển trên đường thẳng \(d\) (\(d ⊥ BC\)). Gọi \(H\) là chân đường cao hạ từ đỉnh \(A\) xuống đường thẳng \(BC.\)
a. Điền vào ô trống trong bảng sau:

b) Vẽ đồ thị biểu diễn số đo \({S_{ABC}}\) theo độ dài AH
c) Diện tích tam giác ABC có tỉ lệ thuận với chiều cao AH không?
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính diện tích tam giác: \(S=\dfrac{1}{2}ah\) với \(h\) là chiều cao tương ứng với cạnh đáy \(a\).
Lời giải chi tiết
a) Ta có \({S_{ABC}} = \dfrac{1}{2}BC.AH \)\(= \dfrac{1}{2}.4.AH = 2AH\)
Ta có bảng sau:

b) \({S_{ABC}}\) là hàm số của chiều cao \(AH.\)
Gọi \(y\) là diện tích của \(∆ ABC\) \(\left( {c{m^2}} \right)\) và độ dài \(x\) là độ dài \(AH\) (cm) thì \(y = 2x\)
Ta có đồ thị như hình sau:
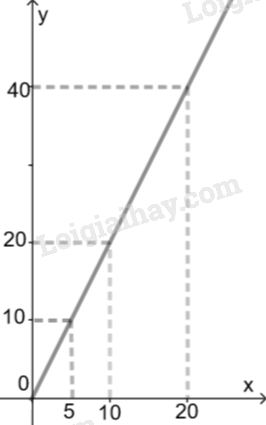
c) Diện tích của tam giác tỉ lệ thuận với chiều cao vì \({S_{ABC}} = k. AH\) ( với k = 2 không đổi)
