LG a
Cho hai tam giác \(ABC\) và \(DBC.\) Kẻ đường cao \(AH\) của tam giác \(ABC.\) Kẻ đường cao \(DK\) của tam giác \(DBC.\) Gọi \(S\) là diện tích của tam giác \(ABC.\) Gọi \(S’\) là diện tích của tam giác \(DBC.\)
Chứng minh rằng \(\dfrac{S}{S'}=\dfrac{DK}{AH}\)
Phương pháp giải:
Áp dụng công thức tính diện tích tam giác: \(S=\dfrac{1}{2}ah\) với \(a;h\) lần lượt là độ dài cạnh đáy và chiều cao tương ứng.
Lời giải chi tiết:
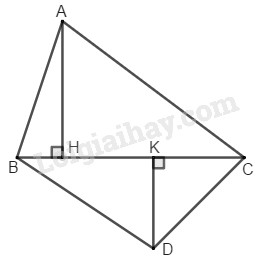
Ta thấy: \(∆ ABC\) và \(∆ DBC\) có chung canh đáy \(BC\) nên ta có:
\(\eqalign{ & {S_{ABC}} = {1 \over 2}AH.BC = S \cr & {S_{DBC}} = {1 \over 2}DK.BC = S' \cr} \)
Suy ra: \(\dfrac{{S'}}{S} = \dfrac{{\dfrac{1}{2}DK.BC}}{{\dfrac{1}{2}AH.BC}}=\dfrac{DK}{AH}\)
LG b
Cho tam giác \(ABC\) và điểm \(M\) bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó là \(AD,\, BE\) và \(CF.\) Đường thẳng đi qua điểm \(M\) và song song với \(AD\) cắt cạnh \(BC\) tại điểm \(H.\) Đường thẳng đi qua điểm \(M\) và song song với \(BE\) cắt cạnh \(AC\) tại điểm \(K.\) Đường thẳng đi qua điểm \(M\) và song song với \(CF\) cắt cạnh \(BA\) tại điểm \(T.\)
Chứng minh rằng \(\dfrac{{MH}}{{AD}} + \dfrac{{MK}}{{BE}} + \dfrac{{MT}}{{CF}} = 1\)
Phương pháp giải:
Áp dụng công thức tính diện tích tam giác: \(S=\dfrac{1}{2}ah\) với \(a;h\) lần lượt là độ dài cạnh đáy và chiều cao tương ứng.
Lời giải chi tiết:
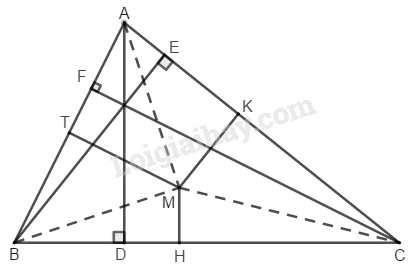
Gọi diện tích các hình tam giác \(ABC,\, MAB,\, MAC, \,MBC\) lần lượt là \(S,\,S_1,\,S_2,\,S_3.\) Ta có:
\(S=S_1+S_2+S_3\)
Trong đó: \(S=\dfrac{1}{2}AD.BC=\dfrac{1}{2}BE.AC\\=\dfrac{1}{2}CF.AB\)
\(\begin{array}{l}
{S_1} = \dfrac{1}{2}MT.AB\\
{S_2} = \dfrac{1}{2}MK.AC\\
{S_3} = \dfrac{1}{2}MH.BC
\end{array}\)
Từ đó, ta có:
\(\begin{array}{l}\dfrac{{{S_1}}}{S} = \dfrac{{\dfrac{1}{2}MT.AB}}{{\dfrac{1}{2}CF.AB}} = \dfrac{{MT}}{{CF}}\\\dfrac{{{S_2}}}{S} = \dfrac{{\dfrac{1}{2}MK.AC}}{{\dfrac{1}{2}BE.AC}} = \dfrac{{MK}}{{BE}}\\\dfrac{{{S_3}}}{S} = \dfrac{{\dfrac{1}{2}MH.BC}}{{\dfrac{1}{2}AD.BC}} = \dfrac{{MH}}{{AD}}\\ \Rightarrow \dfrac{{MH}}{{AD}} + \dfrac{{MK}}{{BE}} + \dfrac{{MT}}{{CF}} \\= \dfrac{{{S_3}}}{S} + \dfrac{{{S_2}}}{S} + \dfrac{{{S_1}}}{S}\\ = \dfrac{{{S_3} + {S_2} + {S_1}}}{S} = \dfrac{S}{S} = 1\end{array}\)
soanvan.me
