Đề bài
Cho góc \(xOy\) khác góc bẹt. Trên tia \(Ox\) lấy hai điểm \(A\) và \(B\) (\(A\) nằm giữa \(O\) và \(B\)), trên tia \(Oy\) lấy hai điểm \(C\) và \(D\) (\(C\) nằm giữa \(O\) và \(D\)). Gọi \( M, N, P, Q\) theo thứ tự là trung điểm của \(AC, BC, BD\), và \(AD.\)
Tìm điều kiện của góc \(xOy\) và các đoạn thẳng \(AB, CD\) để tứ giác \(MNPQ\) là:
a) Hình chữ nhật;
b) Hình thoi;
c) Hình vuông.
Phương pháp giải - Xem chi tiết
Sử dụng:
- Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
- Tứ giác có cặp cạnh đối song song và bằng nhau thì là hình bình hành.
- Hình bình hành có một góc vuông là hình chữ nhật.
- Hình bình hành có hai cạnh kề bằng nhau thì là hình thoi.
- Hình vuông vừa là hình chữ nhật vừa là hình thoi.
Lời giải chi tiết
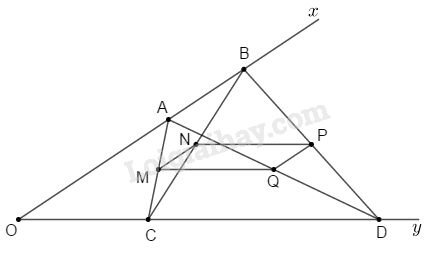
a) \(NP\) là đường trung bình của \(\Delta BCD\) nên \(NP//CD;NP = \dfrac{1}{2}CD\).
\(MQ\) là đường trung bình của \(\Delta ACD\) nên \(MQ//CD;MQ= \dfrac{1}{2}CD\).
Do đó tứ giác \(MNPQ\) có \(NP//MQ\) (cùng song song với \(CD\); \(NP=MQ= \dfrac{1}{2}CD\) nên \(MNPQ\) là hình bình hành.
\(MN\) là đường trung bình của \(\Delta ABC\) nên \(MN//AB;MN = \dfrac{1}{2}AB\).
Vì \( MNPQ\) là hình bình hành mà hình bình hành có một góc vuông là hình chữ nhật nên để \(MNPQ\) là hình chữ nhật thì \(MN\bot \;MQ\) hay \(Ox\bot\,Oy\).
Vậy \(\widehat {xOy} = {90^o}\) thì \(MNPQ\) là hình chữ nhật.
b) Vì \( MNPQ\) là hình bình hành mà hình bình hành có hai cạnh kề bằng nhau là hình thoi nên để \(MNPQ\) là hình thoi thì \(MN=MQ\) hay \(AB=CD\).
Vậy \(MNPQ\) là hình thoi \(⇔ AB = CD.\)
c) \(MNPQ\) là hình vuông khi nó vừa là hình chữ nhật vừa là hình thoi.
Vậy \(MNPQ\) là hình vuông \(⇔ \widehat {xOy} = {90^o}\) và \(AB = CD.\)
soanvan.me
