Đề bài
Cho tam giác ABC có M là giao điểm của hai đường phân giác của góc B và góc C. Cho biết \(\widehat {BMC} = {132^o}\). Tính số đo các góc \(\widehat {MAB}\) và \(\widehat {MAC}\).
Phương pháp giải - Xem chi tiết
Sử dụng tính chất tia phân giác của các góc trong một tam giác để tính số đo góc cần tìm.
Lời giải chi tiết
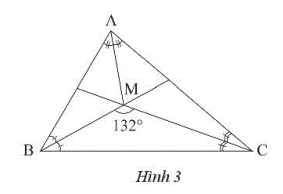
Ta có \(\widehat {MBC} + \widehat {MCB} = {180^o} - \widehat {BMC} = {180^o} - {132^o} = {48^o}\)
Do BM và CM là phân giác các góc \(\widehat B\) và \(\widehat C\) của tam giác ABC nên ta có:
\(\widehat B + \widehat C = 2\left( {\widehat {MBC} + \widehat {MCB}} \right) = {2.48^o} = {96^o}\)
Suy ra: \(\widehat {{A^{}}} = {180^o} - \left( {\widehat B + \widehat C} \right) = {180^o} - {96^o} = {84^o}\)
Do AM là phân giác của góc A của tam giác ABC nên ta có:
\(\widehat {MAB} = \widehat {MAC} = \frac{{\widehat {{A^{}}}}}{2} = \frac{{{{84}^o}}}{2} = {42^o}\)
