Đề bài
Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Chứng minh AH là đường trung trực của BC.
Phương pháp giải - Xem chi tiết
- Chứng minh: \(\Delta ABM = \Delta ACM\) suy ra MB = MC.
Lời giải chi tiết
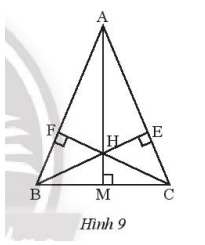
Ta có AH là đường cao vuông góc với cạnh BC tại M.
Xét hai tam giác vuông ABM và ACM có:
Cạnh huyền bằng nhau: AB = AC
Cạnh góc vuông AM chung
Suy ra: \(\Delta ABM = \Delta ACM\) (cạnh huyền – cạnh góc vuông)
Suy ra MB = MC
Vậy AH là đường trung trực của BC
