Đề bài
Trong không gian \(Oxyz\) cho ba vectơ \(\overrightarrow a = ( - 1;1;0)\), \(\overrightarrow b = (1;1;0)\) và \(\overrightarrow c = (1;1;1)\)
Cho hình bình hành \(OADB\) có \(\overrightarrow {OA} \) = \(\overrightarrow a \), \(\overrightarrow {OB} = \overrightarrow b \) (\(O\) là gốc toạ độ). Toạ độ của tâm hình bình hành \(OADB\) là:
(A) \((0 ; 1 ; 0)\) (B) \((1 ; 0 ; 0)\)
(C) \((1 ; 0 ; 1)\) (D) \((1 ; 1 ; 0)\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Gọi I là tâm hình bình hành OADB ta có: \(\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OI} \)
Lời giải chi tiết
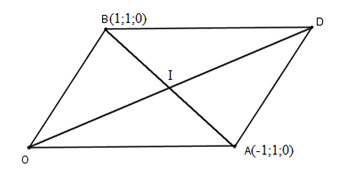
Gọi \(I\) là tâm của hình bình hành ta có:
\(\begin{array}{l}
\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OI} \\
\Rightarrow \overrightarrow {OI} = \dfrac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \dfrac{1}{2}\left( {\overrightarrow a + \overrightarrow b } \right)\\
= \dfrac{1}{2}\left( {0;2;0} \right) = \left( {0;1;0} \right)
\end{array}\)
Vậy \(I(0;1;0)\)
Chọn (A).
Cách khác:
\(\overrightarrow {OA} = \left( { - 1;1;0} \right) \Rightarrow A\left( { - 1;1;0} \right)\)
\(\overrightarrow {OB} = \left( {1;1;0} \right) \Rightarrow B\left( {1;1;0} \right)\)
Vì \(I\) là tâm hình bình hành nên \(I\) là trung điểm \(AB\)
\( \Rightarrow \left\{ \begin{array}{l}{x_I} = \dfrac{{{x_A} + {x_B}}}{2} = \dfrac{{ - 1 + 1}}{2} = 0\\{y_I} = \dfrac{{{y_A} + {y_B}}}{2} = \dfrac{{1 + 1}}{2} = 1\\{z_I} = \dfrac{{{z_A} + {z_B}}}{2} = \dfrac{{0 + 0}}{2} = 0\end{array} \right.\) \( \Rightarrow I\left( {0;1;0} \right)\)
soanvan.me
