Đề bài
Cho hình vuông \(ABCD\) có tâm đối xứng \(O\), cạnh \(a.\) Một góc vuông \(xOy\) có tia \(Ox\) cắt cạnh \(AB\) tại \(E\), tia \(Oy\) cắt cạnh \(BC\) tại \(F\) (h.\(115\))
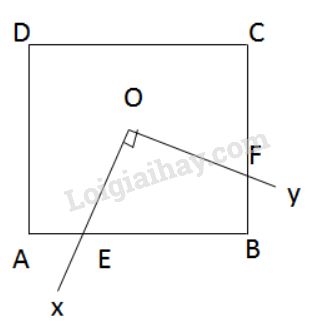
Tính diện tích tứ giác \(OEBF.\)
Phương pháp giải - Xem chi tiết
Áp dụng tính chất hình vuông, công thức tính diện tích hình vuông; diện tích tam giác vuông, tam giác thường.
Diện tích hình vuông cạnh \(a\) bằng \(a^2\)
Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông
Diện tích tam giác bằng nửa tích cạnh đáy và chiều cao tương ứng.
Lời giải chi tiết
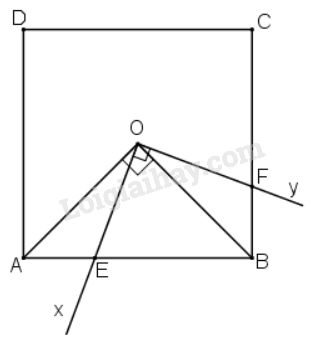
\(O\) là giao điểm hai đường chéo của hình vuông \(ABCD\)
nên \(\widehat {AOB} = 90^o\) và \(OA=OB\).
\(\Delta AOE\) và \(\Delta BOF\) có:
\(\widehat {EAO} = \widehat {FBO} \) (vì \(ABCD\) là hình vuông)
\(OA = OB\) (chứng minh trên)
\(\widehat {AOE} = \widehat {BOF}\) (cùng phụ với \(\widehat {BOE}\))
Do đó \( ∆AOE = ∆BOF\, (g.c.g) \), suy ra \({S_{AOE}} = {S_{BOF}}\)
Cùng cộng với \({S_{EOB}}\) ta được \({S_{AOB}}={S_{OEBF}} \) (1)
Ta lại có \({S_{AOB}}=\dfrac{1}{4}{S_{ABCD}}= \dfrac{1}{4}{a^2}\) (2)
Từ (1) và (2) suy ra \({S_{OEBF}} = \dfrac{1}{4}{a^2}\)
soanvan.me
