Đề bài
Gọi \(O\) là điểm nằm trong hình bình hành \(ABCD.\) Chứng minh rằng tổng diện tích của hai tam giác \(ABO\) và \(CDO\) bằng tổng diện tích của hai tam giác \(BCO\) và \(DAO.\)
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính diện tích tam giác, diện tích hình bình hành.
Diện tích hình bình hành bằng tích một cạnh với chiều cao tương ứng.
Diện tích tam giác bằng nửa tích cạnh đáy và chiều cao tương ứng.
Lời giải chi tiết
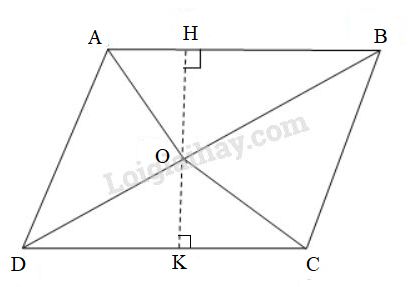
Đặt \(AB=CD=a\). Kẻ \(O{H} ⊥ AB,\) \(OH\) cắt \(CD\) ở \(K.\)
Do \(HK\bot AB\) và \(AB//CD\) nên \(HK\bot CD.\)
Ta có \(OH+OK=HK\)
\({S_{ABO}} + {S_{CDO}} \)
\( = AB.\dfrac{1}{2}O{H} + \dfrac{1}{2}O{K}.CD\)
\( = \dfrac{1}{2}aO{H} + \dfrac{1}{2}a.O{K}\)
\(= \dfrac{1}{2}a\left( {O{H} + O{K}} \right)\)
\(= \dfrac{1}{2}a.{H}{K}\) (1)
\({S_{ABCD}}=AB.HK=a.HK\) (2)
Từ (1) và (2) suy ra
\( \Rightarrow {S_{ABO}} + {S_{CDO}} = \dfrac{1}{2}{S_{ABCD}}\)
Suy ra \({S_{BCO}} + {S_{DAO}} = \dfrac{1}{2}{S_{ABCD}}\)
Vậy \({S_{ABO}} + {S_{CDO}} = {S_{BCO}} + {S_{DAO}}\)
soanvan.me
