Đề bài
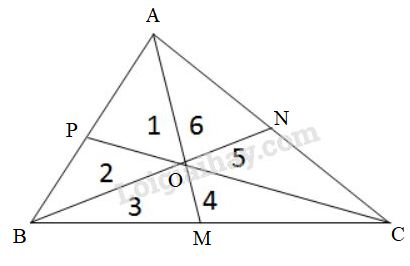
Vẽ ba đường trung tuyến của một tam giác (h.\(120\)). Chứng minh sáu tam giác: \(1, 2, 3, 4, 5, 6\) có diện tích bằng nhau.
Phương pháp giải - Xem chi tiết
Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.
$$S = {1 \over 2}ah$$
Lời giải chi tiết
Trước hết ta sẽ chứng minh \({S_3} = \dfrac{1}{6}{S_{ABC}}\).
Ta có \({S_3} = \dfrac{1}{2}{S_{BOC}}\) (1) ( vì \(BM = \dfrac{1}{2}BC\), chung chiều cao kẻ từ \(O\) đến \(BC\)).
\({S_{BOC}} = \dfrac{2}{3}{S_{BNC}}\) (2) (vì \(BO = \dfrac{2}{3}BN\), chung chiều cao kẻ từ \(C\) đến \(BN\)).
\({S_{BNC}} = \dfrac{1}{2}{S_{ABC}}\) (3) (vì \(NC = \dfrac{1}{2}AC\), chung chiều cao kẻ từ \(B\) đến \(AC\)).
Từ (1), (2), (3) suy ra \({S_3} = \dfrac{1}{2}.\dfrac{2}{3}.\dfrac{1}{2}{S_{ABC}}=\dfrac{1}{6}{S_{ABC}}\)
Chứng minh tương tự, mỗi diện tích \({S_1} ,\, {S_2} ,\, {S_4},\, {S_5},\, {S_6}\) cũng bằng \(\dfrac{1}{6}{S_{ABC}}\).
Vậy \({S_1} = {S_2} = {S_3} = {S_4} = {S_5} = {S_6}\).
soanvan.me
