Đề bài
Cho tam giác \(ABC\), trong đó \(BC=11cm\), \(\widehat{ABC}=38^{\circ},\widehat{ACB}=30^{\circ}.\) Gọi điểm \(N\) là chân của đường vuông góc kẻ từ \(A\) đến cạnh \(BC\). Hãy tính:
a) Đoạn thẳng \(AN\);
b) Cạnh \(AC\).
Gợi ý: Kẻ \(BK\) vuông góc với \(AC\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Tam giác \(ABC\) vuông tại \(A\) thì \(\widehat{B}+\widehat{C}=90^o\).
+) Sử dụng các hệ thức về cạnh và góc trong tam giác vuông: Tam giác \(ABC\) vuông tại \(A\) thì:
\(b=a.\sin B \Rightarrow a=\dfrac{b}{\sin B}\);
\( b= a . \cos C \Rightarrow a=\dfrac{b}{\cos C}\).
Lời giải chi tiết
a) Kẻ \(BK\perp AC\) \((K\in AC)\)
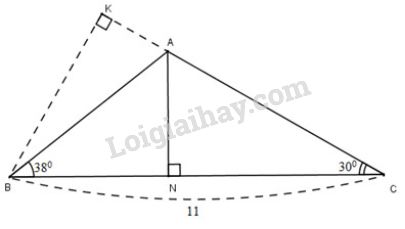
Xét tam giác vuông \(BKC\) ta có:
\(\widehat{KBC}+\widehat{KCB}=90^{\circ}\)
\(\Rightarrow \widehat{KBC}=90^o - \widehat{KCB}=90^o -30^{\circ}=60^{\circ}\)
Mà \(\widehat{KBA}+\widehat{ABN}=\widehat{KBN} \Rightarrow \widehat{KBA}=\widehat{KBN}-\widehat{ABN}\)
\(\Leftrightarrow \widehat{KBA}=60^{\circ}-38^{\circ}=22^{\circ}\)
Xét tam giác \(KBC\) vuông tại \(K\) có:
\(BK=BC\cdot \sin C=11\cdot \sin30^{\circ}=5,5(cm)\)
Xét tam giác \(KBA\) vuông tại \(K\) có:
\(BK=AB. \cos \widehat{KBA} \Leftrightarrow 5,5=AB.\cos 22^o \)
\(\Rightarrow AB=\dfrac{5,5}{\cos 22^{\circ}}\approx 5,932 (cm).\)
Xét tam giác \(ABN\) vuông tại \(N\) có:
\(AN= AB. \sin \widehat{ABN} \approx 5,932.\sin 38^o \approx 3,652(cm)\)
b) Xét tam giác \(ANC\) vuông tại \(N\) có:
\(AN=AC. \sin C \Rightarrow 3,652 = \sin 30^o . AC\)
\(\Leftrightarrow AC=\dfrac{3,652}{\sin 30^o} \approx 7,304(cm)\).
soanvan.me
