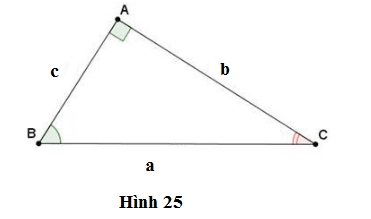
Đề bài
Viết các tỉ số lượng giác của góc B và góc C. Từ đó hãy tính mỗi cạnh góc vuông theo:
a) Cạnh huyền và các tỉ số lượng giác của góc B và góc C;
b) Cạnh góc vuông còn lại và các tỉ số lượng giác của góc B và góc C.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng định nghĩa tỉ số lượng giác của góc nhọn.
\(\sin \alpha =\dfrac{cạnh\ đối}{cạnh\ huyền};\) \(\cos \alpha = \dfrac{cạnh\ kề}{cạnh\ huyền}\);
\(\tan \alpha = \dfrac{cạnh\ đối}{cạnh\ kề};\) \(\cot \alpha =\dfrac{cạnh\ kề}{cạnh\ đối}.\)
Lời giải chi tiết
\(\eqalign{& \sin B = {b \over a};\,\,\cos B = {c \over a};\,\,tgB = {b \over c};\,\,{\mathop{\rm cotgB}\nolimits} = {c \over b} \cr & \sin C = {c \over a};\,\,\cos C = {b \over a};\,\,tgC = {c \over b};\,\,{\mathop{\rm cotgB}\nolimits} = {b \over c} \cr} \)
a)
\(\eqalign{& b = a.\left( {{b \over a}} \right) = a.\sin B = a.\cos C \cr & c = a.\left( {{c \over a}} \right) = a.\cos B = a.\sin C \cr} \)
b)
\(\eqalign{& b = c.\left( {{b \over c}} \right) = c.tgB = c.{\mathop{\rm cotg}\nolimits} C \cr & c = b.\left( {{c \over b}} \right) = b.{\mathop{\rm cotg}\nolimits} B = b.tgC \cr} \)
soanvan.me
