Đề bài
Cho tam giác ABC có \(AB = 11cm,\,\,\widehat {ABC} = {38^o},\,\,\widehat {ACB} = {30^o}\). Gọi N là chân đường cao vuông góc kẻ từ A đến BC. Hãy tính AN và AC (làm tròn đến chữ số thập phân thứ hai).
Phương pháp giải - Xem chi tiết
Vận dụng kiến thức : Trong tam giác vuông, \(\sin \alpha = \dfrac{\text{cạnh đối}}{\text{cạnh huyền}}\) để tìm độ dài của cạnh góc vuông hoặc cạnh huyền.
Lời giải chi tiết
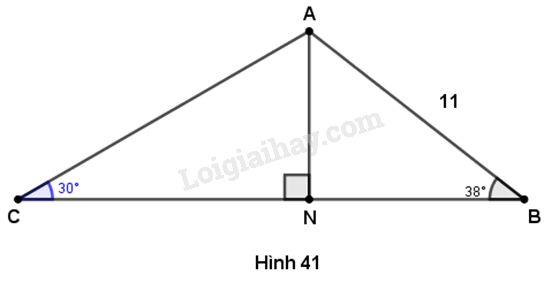
Trong tam giác vuông \(ANB,\) ta có : \(\sin B = \dfrac{{AN}}{{AB}}\) hay \(\sin {38^o} = \dfrac{{AN}}{{11}}\)
Suy ra \(AN = 11.\sin {38^o} \approx 6,77\left( {cm} \right).\)
Trong tam giác vuông \(ANC,\) ta có : \(\sin C = \dfrac{{AN}}{{AC}}\) hay \(\sin {30^o} \approx \dfrac{{6,77}}{{AC}}\)
Suy ra \(AC \approx \dfrac{{6,77}}{{\sin {{30}^o}}} = 13,54\left( {cm} \right).\)
soanvan.me
