Đề bài
Cho tam giác ABC, trong đó AB = 5cm, AC bằng 8cm và \(\widehat {BAC} = {20^o}\) . Hãy dùng các thông tin cho được dưới đây (nếu cần thiết) để tính diện tích tam giác ABC.
\(\sin {20^o} \approx 0,3420;\,\,\cos {20^o} \approx 0,9397;\)\(\tan {20^o} \approx 0,3640\)
Phương pháp giải - Xem chi tiết
- Tìm độ dài chiều cao \(BH\) bằng hệ thức về cạnh huyền và \(\sin \widehat {BAC}\)
- Diện tích tam giác bằng \(\dfrac{1}{2}\) cạnh đáy nhân chiều cao tương ứng.
Lời giải chi tiết
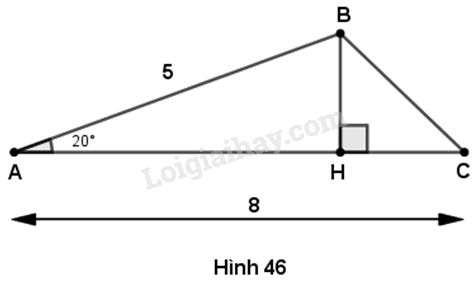
Trong tam giác \(ABC,\) kẻ đường cao \(BH.\) Khi đó :
\({S_{ABC}} = \dfrac{1}{2} \cdot BH \cdot AC\)
Trong tam giác vuông \(AHB,\) ta có \(BH = AB.\sin \widehat {BAC} = 5.\sin {20^o}\)\( \approx 1,71\left( {cm} \right).\)
Vậy diện tích tam giác \(ABC\) là : \({S_{ABC}} \approx \dfrac{1}{2} \cdot 1,71 \cdot 8 \)\(= 6,84\left( {c{m^2}} \right).\)
soanvan.me
