Đề bài
Cho tam giác ABC, trong đó \(BC = 11cm,\,\,\widehat {ABC} = {38^o},\,\,\widehat {ACB} = {30^o}\)..Gọi N là chân đường cao vuông góc kẻ từ A đến cạnh BC. Hãy tính:
a) Đoạn AN
b) Cạnh AC
(Gợi ý: Kẻ BK vuông góc với AC)
Phương pháp giải - Xem chi tiết
- Kẻ thêm đoạn \(BK\) vuông góc với \(AC\) để có tìm độ dài cạnh \(AB.\)
- Vận dụng các tỉ số lượng giác và hệ số về cạnh và góc trong tam giác vuông để tìm độ lớn cạnh \(AN\) và \(AC.\)
Lời giải chi tiết
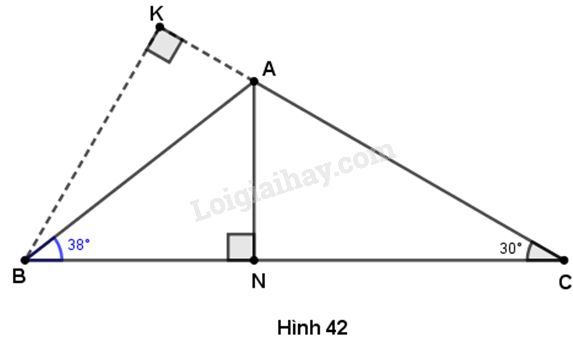
Kẻ \(BK\) vuông góc với \(AC\left( {K \in AC} \right).\) Ta có tam giác \(BKC\) vuông tại \(K.\) Do \(\widehat C = {30^o}\) nên \(\widehat {KBC} = {60^o}.\) Từ đó :
\(BK = BC\sin C = 11\sin {30^o} \)\(= \dfrac{{11}}{2} = 5,5\left( {cm} \right).\)
\(\widehat {KBA} = \widehat {KBC} - \widehat {ABC}\)\( = {60^o} - {38^o} = {22^o}.\)
Trong tam giác vuông \(ABK,\) biết \(BK = 5,5cm\) và \(\widehat {KBA} = {22^o},\) do đó \(AB = BK:\cos \widehat {ABK} = 55:\cos {22^o}\)\( \approx 5,932\left( {cm} \right).\)
a) Trong tam giác vuông \(ANB,\) ta có \(AN = AB.\sin \widehat {ABC} \)\(\approx 5,932.\sin {38^o} \approx 3,652\left( {cm} \right).\)
b) Trong tam giác vuông \(ANC,\) ta có : \(AC = AN:\sin \widehat {ACB}\)\( \approx 3,652:\sin {30^o} \approx 7,304\left( {cm} \right).\)
soanvan.me
