Đề bài
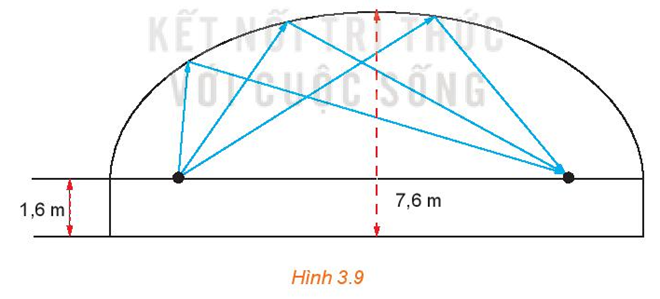
Một phòng thì thầm có trần vòm elip với hai tiêu điểm ở độ cao 1,6m (so với mặt sàn) và cách nhau 16m. Đỉnh của mái vòm cao 7,6 m (H.3.9). Hỏi âm thanh thì thầm từ một tiêu điểm thì sau bao nhiêu giây đến được tiêu điểm kia? Biết vận tốc âm thanh là 343,2 m/s và làm tròn đáp số tới 4 chữ số sau dấu phẩy.
Phương pháp giải - Xem chi tiết
Cho PTCT: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), \({F_1}( - c;0)\) là một tiêu điểm.
+ Khoảng cách giữa 2 tiêu điểm: 2c
+ M bất kì thuộc elip, ta có: \(M{F_1} + M{F_2} = 2a\)
Lời giải chi tiết
Gọi PTCT của mái vòm đó là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\),
+ Khoảng cách giữa 2 tiêu điểm: 2c = 16 (m) \( \Rightarrow c = 8\)
+ Nửa độ dài trục nhỏ là \(b = 7,6 - 1,6 = 6.\)
\( \Rightarrow a = \sqrt {{c^2} + {b^2}} = 10\)
+ M bất kì thuộc elip, ta có: \(M{F_1} + M{F_2} = 2a\) (\({F_1},{F_2}\) là hai tiêu điểm)
Quãng đường âm thanh thì thầm từ tiêu điểm này đến tiêu điểm kia là \(20(m)\)
Thời gian âm thanh thì thầm từ tiêu điểm này đến tiêu điểm kia là: \(\frac{{20}}{{343,2}} \approx 0,0583\;(s)\)
Vậy mất khoảng 0,0583 giây để âm thanh thì thầm từ tiêu điểm này đến được tiêu điểm kia.
