HĐ1
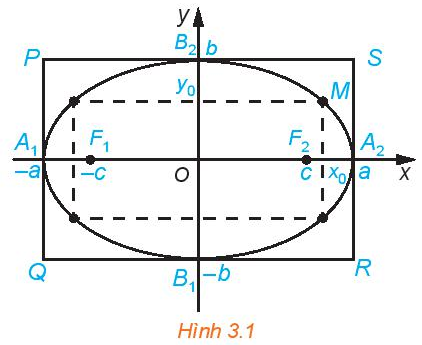
Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (H.3.1)
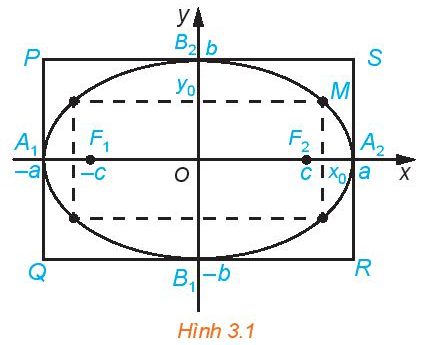
a) Tìm tọa độ các giao điểm của elip với các trục tọa độ
b) Hãy giải thích vì sao, nếu điểm \(M({x_0};{y_0})\) thuộc elip thì các điểm có tọa độ \(({x_0}; - {y_0}),( - {x_0};{y_0}),( - {x_0}; - {y_0})\) cũng thuộc Elip.
c) Với điểm \(M({x_0};{y_0})\) thuộc elip, hãy so sánh \(O{M^2}\) với \({a^2},{b^2}\)
Lời giải chi tiết:
a)
\(y = 0 \Rightarrow \frac{{{x^2}}}{{{a^2}}} = 1 \Rightarrow x = \pm a\)
Giao điểm của elip với Ox là \({A_1}\left( { - a;0} \right),{A_2}\left( {a;0} \right).\)
\(x = 0 \Rightarrow \frac{{{y^2}}}{{{b^2}}} = 1 \Rightarrow y = \pm b\)
Giao điểm của elip với Oy là \({B_1}\left( {0; - b} \right),{B_2}\left( {0;b} \right).\)
b) Nếu điểm \(M({x_0};{y_0})\) thuộc elip thì \(\frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} = 1\)
\( \Rightarrow \frac{{{x_0}^2}}{{{a^2}}} + \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1;\frac{{{{( - {x_0})}^2}}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} = 1;\frac{{{{( - {x_0})}^2}}}{{{a^2}}} + \frac{{{{( - {y_0})}^2}}}{{{b^2}}} = 1\)
hay các điểm có tọa độ \(({x_0}; - {y_0}),( - {x_0};{y_0}),( - {x_0}; - {y_0})\) cũng thuộc Elip.
c) Từ H.3.1 dễ thấy \(a > b\)
\(\begin{array}{l} \Rightarrow \frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{a^2}}} \le \frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} \le \frac{{{x_0}^2}}{{{b^2}}} + \frac{{{y_0}^2}}{{{b^2}}}\\ \Leftrightarrow \frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{a^2}}} \le 1 \le \frac{{{x_0}^2}}{{{b^2}}} + \frac{{{y_0}^2}}{{{b^2}}}\\ \Leftrightarrow {b^2} \le {x_0}^2 + {y_0}^2 \le {a^2}\\ \Leftrightarrow {b^2} \le O{M^2} \le {a^2}\end{array}\)
Luyện tập 1
Viết phương trình chính tắc của elip với độ dài trục lớn bằng 10 và tiêu cự bằng 6.
Phương pháp giải:
Phương trình chính tắc của elip \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Trong đó:
+ Độ dài trục lớn: \(2a\)
+ Tiêu cự: \(2c = 2\sqrt {{a^2} - {b^2}} \)
Lời giải chi tiết:
Ta có:
+ Độ dài trục lớn: \(2a = 10 \Rightarrow a = 5\)
+ Tiêu cự: \(2c = 2\sqrt {{a^2} - {b^2}} = 6 \Rightarrow \sqrt {{5^2} - {b^2}} = 3 \Rightarrow {b^2} = 16\)
Phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)
Luyện tập 2
(Phép co đường tròn) Cho đường tròn có phương trình \({x^2} + {y^2} = {a^2}\) và số k \((0 < k < 1)\). Với mỗi điểm \(M({x_0};{y_0})\) thuộc đường tròn, gọi \(H({x_0};0)\) là hình chiếu vuông góc của M lên trục Ox và N là điểm thuộc đoạn MH sao cho \(HN = kHM\) (H.3.5)
a) Tính tọa độ của N theo \({x_0};{y_0};k.\)
b) Chứng minh rằng khi điểm M thay đổi trên đường tròn thì N thay đổi trên Elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{{(ka)}^2}}} = 1\)
Lời giải chi tiết:
Gọi \(N({x_N};{y_N})\).
N thuộc đoạn MH và \(HN = kHM \Rightarrow \overrightarrow {HN} = k\overrightarrow {HM} \)
\(\begin{array}{l} \Leftrightarrow ({x_N} - {x_0};{y_N}) = k(0;{y_0})\\ \Leftrightarrow \left\{ \begin{array}{l}{x_N} - {x_0} = k.0\\{y_N} = k.{y_0}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_N} = {x_0}\\{y_N} = k.{y_0}\end{array} \right.\end{array}\)
Vì \(M({x_0};{y_0})\) thuộc (C) \({x^2} + {y^2} = {a^2}\) nên
\({x_0}^2 + {y_0}^2 = {a^2} \Leftrightarrow {x_N}^2 + {\left( {\frac{{{y_N}}}{k}} \right)^2} = {a^2} \Leftrightarrow \frac{{{x_N}^2}}{{{a^2}}} + \frac{{{y_N}^2}}{{{{(ka)}^2}}} = 1\)
Vậy N thuộc Elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{{(ka)}^2}}} = 1\)
