Đề bài
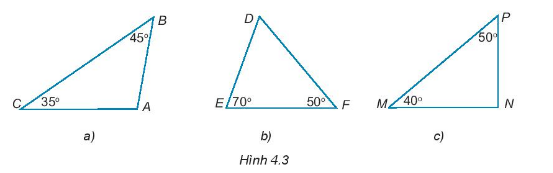
Hãy tính các số đo các góc A, D, N trong các tam giác dưới đây (H.4.3). Trong các tam giác đó, hãy chỉ ra tam giác nào là nhọn, tù, vuông.
Phương pháp giải - Xem chi tiết
-Áp dụng tổng 3 góc trong 1 tam giác bằng 180 độ.
-Tam giác tù khi có 1 góc lớn hơn 90 độ
-Tam giác vuông khi có 1 góc bằng 90 độ
-Tam giác nhọn khi 3 góc đều nhọn (mỗi góc đều nhỏ hơn 90 độ)
Lời giải chi tiết
a) Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^0}\\ \Rightarrow \widehat A + {45^0} + {35^0} = {180^0}\\ \Rightarrow \widehat A = {180^0} - {80^0}\\ \Rightarrow \widehat A = {100^0} > {90^0}\end{array}\)
Tam giác ABC là tam giác tù.
b) Áp dụng định lí tổng ba góc trong tam giác DEF, ta có:
\(\begin{array}{l}\widehat D + \widehat E + \widehat F = {180^0}\\ \Rightarrow \widehat D + {70^0} + {50^0} = {180^0}\\ \Rightarrow \widehat D = {180^0} - {120^0}\\ \Rightarrow \widehat D = {60^0} < {90^0}\end{array}\)
Tam giác DEF là tam giác nhọn vì cả 3 góc đều nhọn.
c) Áp dụng định lí tổng ba góc trong tam giác MNP, ta có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^0}\\ \Rightarrow {40^0} + \widehat N + {50^0} = {180^0}\\ \Rightarrow \widehat N = {180^0} - {90^0}\\ \Rightarrow \widehat N = {90^0}\end{array}\)
Tam giác MNP vuông tại N.
