Đề bài
Tính tổng số đo \(\widehat A + \widehat C\) trong hình 4.8.
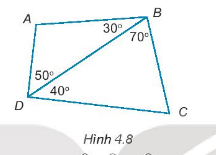
Phương pháp giải - Xem chi tiết
Áp dụng tổng ba góc trong 1 tam giác bằng 180 độ chỉ ra số đo góc A, C.
Lời giải chi tiết
Cách 1:
Áp dụng định lí tổng ba góc trong tam giác ABD, ta có:
\(\widehat A+ \widehat B+ \widehat C=180^0\Rightarrow \widehat A = {180^0} - {50^0} - {30^0} = {100^0}\)
Áp dụng định lí tổng ba góc trong tam giác BCD, ta có:
\(\widehat B+ \widehat C+ \widehat D=180^0\Rightarrow \widehat C = {180^0} - {40^0} - {70^0} = {70^0}\)
\(\widehat A + \widehat C = {100^0} + {70^0} = {170^0}\)
Cách 2:
Áp dụng định lí tổng ba góc trong tam giác ABD, ta có:
\(\widehat A+ \widehat B+ \widehat C=180^0 \Rightarrow \widehat A+ 30^0+50^0=180^0\)
Áp dụng định lí tổng ba góc trong tam giác BCD, ta có:
\(\widehat B+ \widehat C+ \widehat D=180^0 \Rightarrow \widehat 70^0+ \widehat C+40^0=180^0\)
Do đó, \(\widehat A+ 30^0+50^0+\widehat 70^0+ \widehat C+40^0=180^0+180^0\) nên \(\widehat A + \widehat C =170^0\)
