Đề bài
Cho hình bình hành \(ABCD\) tâm \(O\). Gọi \(K,\,\,L,\,\,M,\,\,N\) tướng ứng là trung điểm các cạnh \(AB,\,\,BC,\,\,CD,\,\,DA.\) Trong các vectơ có đầu mút lấy từ các điểm \(A,\,\,B,\,\,C,\,\,D,\,\,K,\)\(L,\,\,M,\,\,O\) có bao nhiêu vectơ bằng vectơ \(\overrightarrow {AK} \) ?
A. 2
B. 6
C. 4
D. 8
Phương pháp giải - Xem chi tiết
Liệt kê các vectơ có cùng độ dài và cùng hướng với vectơ \(\overrightarrow {AK} \)
Lời giải chi tiết
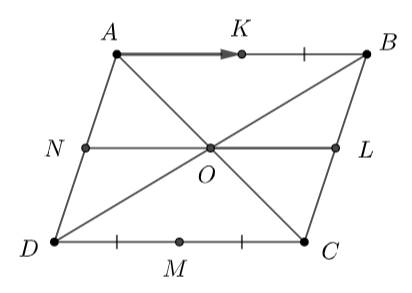
Xét hình bình hành \(ABCD\):
\( \Rightarrow \) \(AB = CD\)
mặt khác \(K\) và \(M\) lần lượt là trung điểm của \(AB\) và \(CD\)
nên \(AK = KB = CM = DM\) (1)
Ta có: \(NL\) là đường trung bình của hình bình hành \(ABCD\)
\( \Rightarrow \) \(NL\)//\(AB\)
Mặt khác \(AN\)//\(BL\)
\( \Rightarrow \) tứ giác \(ABLN\) là hình bình hành
\( \Rightarrow \) \(AB = NL\)
Ta có: \(O\) là trung điểm của \(NL\)
\(K\) là trung điểm của \(AB\)
Mặt khác \(AB = NL\)
\( \Rightarrow \) \(AK = NO = OL = AB\) (2)
Từ (1) và (2) \( \Rightarrow \) \(AK = KB = NO = OL = DM = MC\)
Mà các đường thẳng \(KB,\) \(NO,\) \(OL,\) \(DM,\) \(MC\) đều song song với \(AK\)
\( \Rightarrow \) \(\overrightarrow {AK} = \overrightarrow {KB} = \overrightarrow {NO} = \overrightarrow {OL} = \overrightarrow {DM} = \overrightarrow {MC} \)
Có 6 vectơ bằng vectơ \(\overrightarrow {AK} \)
Chọn B.
