Đề bài
Tính số đo các góc x, y, z, t, v trong hình 4.55
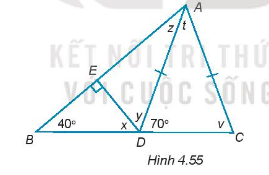
Phương pháp giải - Xem chi tiết
-Trong tam giác vuông tổng hai góc còn lại bằng 90 độ
-Tổng 3 góc trong 1 tam giác bằng 180 độ
Lời giải chi tiết
Vì tam giác BED vuông tại E nên \(x+40^0=90^0 \Rightarrow x = {90^0} - {40^0} = {50^0}\).
Vì \(x+y+70^0=180^0 \Rightarrow y = {180^0} - x - {70^0} = {60^0}\).
Vì tam giác AED vuông tại E nên \(z+y=90^0 \Rightarrow z = {90^0} - y = 90^0-60^0={30^0}\).
Vì tam giác ADC có AC = AD nên là tam giác cân tại A \(\Rightarrow v = {70^0}\).
Áp dụng định lí tổng ba góc trong một tam giác trong tam giác ADC, có:
\(v+70^0+t=180^0 \\\Rightarrow t = {180^0} - {70^0} - v ={180^0} - {70^0}-70^0= {40^0}\).
Vậy \(x=50^0;y=60^0;z=30^0; v=70^0;t=40^0\).
