Đề bài
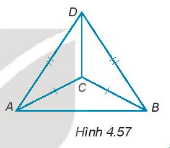
Cho các điểm A, B, C, D như Hình 4.57
a) Chứng minh rằng \(\widehat {DAC} = \widehat {DBC}\).
b) Đường thẳng DC có vuông góc với đường thẳng AB không? Vì sao?
Phương pháp giải - Xem chi tiết
a) Chứng minh: \(\Delta DAC = \Delta DBC\left( {c - c - c} \right)\)
b) Điểm cách đều 2 đầu mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Lời giải chi tiết
a)
Xét \(\Delta DAC\) và \(\Delta DBC\) có:
DA = DB
AC = BC
CD: Cạnh chung
\(\begin{array}{l} \Rightarrow \Delta DAC = \Delta DBC\left( {c - c - c} \right)\\ \Rightarrow \widehat {DAC} = \widehat {DBC}\end{array}\)
b)
Điểm D và C cùng cách đều A và B nên đường thẳng DC là đường trung trực của đoạn thẳng AB. Do đó đường thẳng DC vuông góc với đường thẳng AB
