Đề bài
Cho Hình 4.61, hãy tính số đo các góc của tam giác ABE.
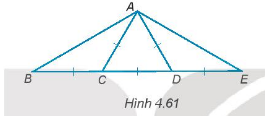
Phương pháp giải - Xem chi tiết
-Tính các góc của tam giác ACD
-Tính các góc ABC, BAC (Tam giác ABC cân tại C)
-Tính các góc AED, DAE (Tam giác ADE cân tại D).
Lời giải chi tiết
Tam giác ACD đều, nên \(\widehat {ACD} = \widehat {ADC} = \widehat {CAD} = {60^0}\)
Tam giác ABC cân tại đỉnh C nên:
\(\widehat {ABC} = \widehat {BAC} = \dfrac{{\widehat {ABC} + \widehat {BAC}}}{2} = \dfrac{{{{180}^0} - \widehat {ACB}}}{2} = \dfrac{{\widehat {ACD}}}{2} = {30^0}.\)
Tam giác ADE cân tại đỉnh D nên:
\(\widehat {AED} = \widehat {DAE} = \dfrac{{\widehat {AED} + \widehat {DAE}}}{2} = \dfrac{{{{180}^0} - \widehat {ADE}}}{2} = \dfrac{{\widehat {ADC}}}{2} = {30^0}\)
Do vậy, ta có:
\(\widehat {ABE} = \widehat {ABC} = {30^0};\widehat {AEB} = \widehat {AED} = {30^0};\widehat {BAE} = {180^0} - \widehat {ABE} - \widehat {AEB} = {120^0}\).
