Video hướng dẫn giải
Cho hàm số \(y = 2x^2 + 2mx + m -1\) có đồ thị là \((C_m)\), \(m\) là tham số.
LG a
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi \(m = 1\)
Phương pháp giải:
* Tập xác định
Tìm tập xác định của hàm số
* Sự biến thiên của hàm số
- Xét chiều biến thiên của hàm số
+ Tính đạo hàm \(y’\)
+ Tại các điểm đó đạo hàm \(y’\) bằng 0 hoặc không xác định
+ Xét dấu đạo hàm \(y’\) và suy ra chiều biến thiên của hàm số.
- Tìm cực trị
- Tìm các giới hạn tại vô cực, các giới hạn vô cực và tìm tiệm cận (nếu có)
- Lập bảng biến thiên (Ghi các kết quả tìm được vào bảng biến thiên)
* Đồ thị
Dựa vào bảng biến thiên và các yếu tố xác định ở trên để vẽ đồ thị,
- Nếu hàm số tuần hoàn với chu kì \(T\) thì chỉ cần khảo sát sự biến thiên và vẽ đồ thị trên một chu kì, sau đó tịnh tiến đồ thị song song với trục \(Ox\)
- Nên tính thêm tọa độ một số điểm, đặc biệt là tọa độ các giao điểm của đồ thị với các trục tọa độ.
- Nêu lưu ý đến tính chẵn , tính lẻ của hàm số và tính đối xứng của đồ thị để vẽ cho chính xác.
Lời giải chi tiết:
\(y = 2x^2 + 2mx + m -1\) \((C_m)\). Đây là hàm số bậc hai, có đồ thị là parabol, bề lõm quay lên trên.
a) Với \(m = 1\) ta có hàm số: \(y = 2x^2+ 2x.\)
Tập xác định \(D =\mathbb R\)
* Sự biến thiên:
Ta có: \(y'=4x+2.\)
\(\Rightarrow y'=0 \Leftrightarrow 4x + 2 = 0 \Leftrightarrow x = \dfrac {-1} {2} \)
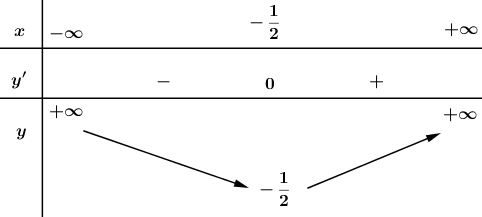
+) Hàm số đồng biến trên khoảng \(\left( \dfrac {-1} {2};+\infty \right)\), nghịch biến trên khoảng \(\left(-\infty; \dfrac {-1} {2}\right)\)
+) Cực trị:
Hàm số đạt cực tiểu tại \(x= \dfrac {-1} {2}\); \(y_{CT}= \dfrac {-1} {2}\)
+) Giới hạn:
\(\mathop {\lim }\limits_{x \to \pm \infty } y = + \infty \)
Bảng biến thiên:
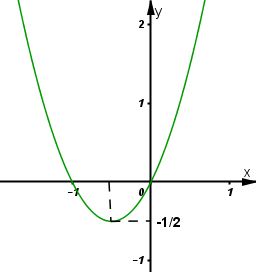
* Đồ thị
Đồ thị hàm số giao trục \(Ox\) tại hai điểm \((-1;0)\) và \((0;0)\)
Cắt \(Oy\) tại \((0;0).\)
LG b
b) Xác định m để hàm số:
- Đồng biến trên khoảng \((-1, +∞)\)
- Có cực trị trên khoảng \((-1, +∞)\)
Phương pháp giải:
+) Hàm số đồng biến trên \( (a; \, b) \Leftrightarrow y' > 0\;\;\forall x \ne \left( {a;\;b} \right).\)
+) Hàm số nghịch biến trên \( (a; \, b) \Leftrightarrow y' < 0\;\;\forall x \ne \left( {a;\;b} \right).\)
Lời giải chi tiết:
Tổng quát \(y = 2x^2+ 2mx + m -1\) có tập xác định \(D = \mathbb R\)
Có \(y' = 4x + 2m = 0 \Rightarrow y'=0 \)
\(\Leftrightarrow 4x+2m=0 \Leftrightarrow x = \dfrac {-m} {2}\)
Suy ra \(y’ >\) 0 với \(x > \dfrac {-m} {2};y' < 0\) với \(x < \dfrac {-m} {2}\) , tức là hàm số nghịch biến trên \(( - \infty ; \dfrac {-m} {2})\) và đồng biến trên \(( \dfrac {-m} {2}; + \infty )\)
i) Để hàm số đồng biến trên khoảng \((-1, +∞)\) thì phải có điều kiện \(( - 1;{\rm{ }} + \infty ) \subset ( \dfrac {-m} {2}; + \infty )\)
\( \Leftrightarrow \dfrac {-m} {2} \le - 1 \Leftrightarrow m \ge 2\)
ii) Hàm số đạt cực trị tại \(x = \dfrac {-m} {2}\) .
Để hàm số đạt cực trị trong khoảng \((-1; +∞)\), ta phải có:
\(\eqalign{
& \dfrac {-m} {2} \in ( - 1, + \infty ) \cr
& \Leftrightarrow \dfrac {-m} {2} > - 1 \Leftrightarrow 1 > \dfrac {m} {2} \Leftrightarrow m < 2 \cr} \)
LG c
c) Chứng minh rằng \((C_m)\) luôn cắt trục hoành tại hai điểm phân biệt với mọi \(m\).
Phương pháp giải:
Đồ thị hàm số \((C_m)\) cắt trục hoành tại hai điểm phân biệt với mọi \(m \Leftrightarrow y=f(x)=0\) có hai nghiệm phân biệt với mọi \(m.\)
Lời giải chi tiết:
\((C_m)\) luôn cắt \(Ox\) tại hai điểm phân biệt \(x = \dfrac {-m} {2}\)
\(⇔\) phương trình \(2x^2+ 2mx + m – 1 = 0\) có hai nghiệm phân biệt.
Ta có: \(Δ’ = m^2– 2m + 2 \) \(= (m-1)^2+ 1 > 0, \, ∀m\)
Vậy \((C_m)\) luôn cắt \(O x\) tại hai điểm phân biệt.
Cách khác
Nhận thấy: \( - \dfrac{{{m^2}}}{2} + m - 1\)\( = - \dfrac{1}{2}\left( {{m^2} - 2m + 2} \right)\)\( = - \dfrac{1}{2}{\left( {m - 1} \right)^2} - \dfrac{1}{2} < 0\) với mọi m.
Suy ra, giá trị cực tiểu luôn nhỏ hơn 0 với mọi \(m\).
Dựa vào bảng biến thiên suy ra đường thẳng \(y = 0\) (trục hoành) luôn cắt đồ thị hàm số tại 2 điểm phân biệt (đpcm).
soanvan.me