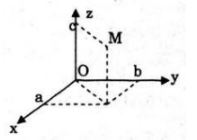
Cho điểm \(M\left( {a;b;c} \right)\).
LG a
Tìm toạ độ hình chiếu (vuông góc) của M trên các mặt phẳng toạ độ và trên các trục toạ độ.
Phương pháp giải:
Dựng hình suy ra tọa độ các điểm.
Lời giải chi tiết:
Hình chiếu của M lên mp(Oxy) tọa độ là: \(M_1\)(a, b, 0)
Tương tự, hình chiếu của M lên mp(Oxz) và mp(Oyz) lần lượt có tọa độ là: \(M_2\)(a, 0, c) và \(M_3\)(0, b, c).
Hình chiếu của M lên các trục Ox, Oy, Oz lần lượt có tọa đố là: \(M_4\)(a, 0, 0), \(M_5\)(0, b, 0), \(M_6\)(0, 0, c).
LG b
Tìm khoảng cách từ điểm M đến các mặt phẳng toạ độ, đến các trục toạ độ.
Lời giải chi tiết:
Khoảng cách từ M đến (Oxy) là:
\(\eqalign{
& d\left( {M;\left( {Oxy} \right)} \right) = M{M_1} \cr &= \sqrt {{{\left( {a - a} \right)}^2} + {{\left( {b - b} \right)}^2} + {{\left( {c - 0} \right)}^2}} = \left| c \right| \cr
& d\left( {M;\left( {Oyz} \right)} \right) = \left| a \right|;d\left( {M;\left( {Oxz} \right)} \right) = \left| b \right| \cr
& d\left( {M;Ox} \right) = M{M_4} \cr &= \sqrt {{{\left( {a - a} \right)}^2} + {{\left( {b - 0} \right)}^2} + {{\left( {c - 0} \right)}^2}} \cr &= \sqrt {{b^2} + {c^2}} \cr
& d\left( {M;Oy} \right) = \sqrt {{a^2} + {c^2}} ,\cr & d\left( {M;Oz} \right) = \sqrt {{a^2} + {b^2}} \cr} \)
LG c
Tìm toạ độ của các điểm đối xứng với M qua các mặt phẳng toạ độ.
Lời giải chi tiết:
Gọi \(M_1'\left( {x;y;z} \right)\) là điểm đối xứng của M qua mp(Oxy) thì \({M_1}\) là trung điểm của \(MM_1'\) nên
\(\left\{ \matrix{
{x_{{M_1}}} = {{{x_M} + {x_{M_1'}}} \over 2} \hfill \cr
{y_{{M_1}}} = {{{y_M} + {y_{M_1'}}} \over 2} \hfill \cr
{z_{{M_1}}} = {{{z_M} + {z_{M_1'}}} \over 2} \hfill \cr} \right. \) \(\Leftrightarrow \left\{ \matrix{
{x_{M_1'}} = 2{x_{{M_1}}} - {x_M} = 2a - a = a \hfill \cr
{y_{M_1'}} = 2{y_{{M_1}}} - {y_M} = 2b - b = b \hfill \cr
{z_{M_1'}} = 2{z_{{M_1}}} - {z_M} = 0 - c = - c \hfill \cr} \right. \) \(\Rightarrow M_1'\left( {a;b; - c} \right)\)
Tương tự \(M_2'\left( { - a;b;c} \right)\) là điểm đối xứng của M qua mp(Oyz)
Và \(M_3'\left( {a; - b;c} \right)\) là điểm đối xứng của M qua mp(Oxz).
soanvan.me