Đề bài
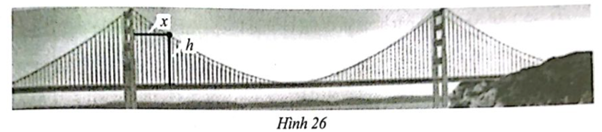
Quan sát chiếc Cổng Vàng (Golden Gate bridge) ở Hình 26. Độ cao \(h\) (feet) tính từ mặt cầu đến các điểm trên dây treo ở phần giữa hai trụ cầu được xác định bởi công thức \(h\left( x \right) = \frac{1}{{9000}}{x^2} - \frac{7}{{15}}x + 500\), trong đó \(x\) (feet) là khoảng cách từ trụ cầu bên trái đến điểm tương ứng trên dây treo
a) Xác định độ cao của trụ cầu so với mặt cầu theo đơn vị feet.
b) Xác định khoảng cách giữa hai trụ cầu theo đơn vị feet, biết rằng hai trụ cầu này có độ cao bằng nhau
Phương pháp giải - Xem chi tiết
Từ công thức ta tính toán các yêu cầu đề bài
Parabol \(y = a{x^2} + bx + c\): có trục đối xứng là đường thẳng \(x = - \frac{b}{{2a}}\)
Lời giải chi tiết
a) Độ cao của trụ cầu ứng với độ cao h tại \(x = 0\)
Tại \(x = 0\) thì \(h\left( 0 \right) = \frac{1}{{9000}}.0 - \frac{7}{{15}}.0 + 500 = 500\) (feet)
Vậy độ cao của trụ cầu so với mặt cầu là 500 feet.
b)
Dễ thấy hai đỉnh trụ cầu đối xứng với nhau qua trục đối xứng của parabol \(h(x)\).
Xác định trục đối xứng của parabol: \(x = \frac{{ - b}}{{2a}} = - \frac{{ - \frac{7}{{15}}}}{{2.\frac{1}{{9000}}}} = 2100\)
Khoảng cách giữa hai trụ cầu là \(2.2100 = 4200\) (feet)
Cách 2:
Do hai trụ cầu cao bằng nhau nên độ cao của trụ cầu bên phải cũng là 500 feet.
Khoảng cách giữa hai trụ cầu chính là hoành độ (khác 0) của trụ cầu bên phải.
Ta tìm \(x \ne 0\) sao cho \(h(x) = 500\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\\frac{1}{{9000}}{x^2} - \frac{7}{{15}}x + 500 = 500\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\\frac{1}{{9000}}{x^2} - \frac{7}{{15}}x = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\\frac{1}{{9000}}x - \frac{7}{{15}} = 0\end{array} \right. \Leftrightarrow x = \frac{7}{{15}}:\frac{1}{{9000}} = 4200\end{array}\)
Vậy khoảng cách giữa hai trụ là 4200 feet.
