Đề bài
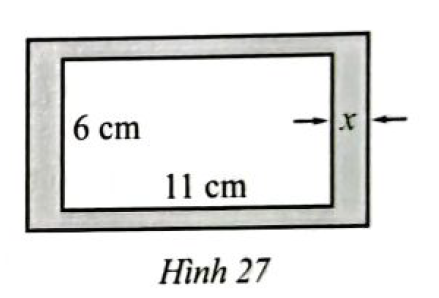
Bác Nam dự định làm một khung ảnh hình chữ nhật sao cho phần trong của khung là hình chữ nhật có kích thước 6 cm x 11 cm, độ rộng viền xung quanh là \(x\) cm (Hình 27). Diện tích của viền khung ảnh không vượt quá \(38c{m^2}\). Hỏi độ rộng viền khung ảnh lớn nhất là bao nhiêu cm?
Phương pháp giải - Xem chi tiết
Đặt độ rộng của viền khung ảnh là \(x\)(cm) (\(x > 0\)). Biểu diễn diện tích viền khung ảnh và giải bất phương trình
Lời giải chi tiết
Đặt độ rộng của viền khung ảnh là \(x\)(cm) (\(x > 0\)).
Ta có diện tích viền khung ảnh là \(\left( {11 + 2x} \right)\left( {6 + 2x} \right) - 66 = 4{x^2} + 34x\) (\(c{m^2}\))
Theo đề bài ta có: \(4{x^2} + 34x \le 38 \Leftrightarrow 4{x^2} + 34x - 38 \le 0\)
Tam thức bậc hai \(4{x^2} + 34x - 38\) có hai nghiệm \({x_1} = \frac{{ - 19}}{2};{x_2} = 1\) và có hệ số \(a = 4 > 0\)
Sử dụng định lý về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của \(x\) sao cho tam thức \(4{x^2} + 34x - 38\) mang dấu “-” là \(\left[ {\frac{{ - 19}}{2};1} \right]\)
Do đó \(0 < x \le 1\)
Vậy độ rộng viền khung ảnh lớn nhất là 1 cm.
