Đề bài
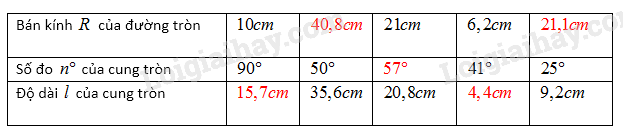
Lấy giá trị gần đúng của \(π\) là \(3,14\), hãy điền vào ô trống trong bảng sau (làm tròn kết quả đến chữ số thập phân thứ nhất và đến độ):
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Cho đường tròn bán kính \(R\). Khi đó:
Độ dài cung có số đo \(n^0\) của đường tròn là: \(l = \dfrac{{\pi Rn}}{{180}}.\)
Suy ra \(n = \dfrac{{180l}}{{\pi R}};\,R = \dfrac{{180l}}{{\pi n}}\)
Lời giải chi tiết
Vận dụng công thức: \(l = \dfrac{\pi Rn}{180}\) để tìm \(R\) hoặc \(n^0\) hoặc \(l\).
Ta có: \(R = \dfrac{{180l}}{{\pi n}};\;\;n = \dfrac{{180l}}{{\pi R}}.\)
+ Với \(R = 10cm;n^\circ = 90^\circ \) thì độ dài cung tròn là \(l = \dfrac{{\pi Rn}}{{180}} = \dfrac{{\pi .10.90}}{{180}} =15,7cm\)
+ Với \(l = 35,6cm;n^\circ = 50^\circ \) thì bán kính đường tròn là \(R = \dfrac{{180l}}{{\pi n}} = \dfrac{{180.35,6}}{{\pi .50}} \approx 40,8cm\)
+ Với \(R = 21cm;l = 20,8cm\) thì số đo \(n^\circ \) của cung tròn là \(n = \dfrac{{180l}}{{\pi R}} = \dfrac{{180.20,8}}{{\pi .21}} \approx 57^\circ \)
+ Với \(R = 6,2;n^\circ = 41^\circ \) thì độ dài cung là \(l = \dfrac{{\pi Rn}}{{180}} = \dfrac{{\pi .6,2.41}}{{180}} \approx 4,4cm\)
+ Với \(n^\circ = 25^\circ ;l = 9,2cm\) thì bán kính của đường tròn là \(R = \dfrac{{180l}}{{\pi n}} = \dfrac{{180.9,2}}{{\pi .25}} \approx 21,1cm\)
Thay số vào, tính toán ta tìm được các giá trị chưa biết trong ô trống và điền vào bảng sau:
soanvan.me

