Đề bài
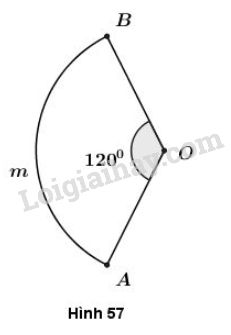
Xem hình 57 và so sánh độ dài của cung \(AmB\) với độ dài đường gấp khúc \(AOB\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Độ dài cung có số đo \(n^0\) của đường tròn bán kính \(R\) là \(l=\dfrac{\pi Rn}{180}\)
Lời giải chi tiết
Ta có góc AOB là góc ở tâm chắn cung AmB nên \(sđ \overparen{AmB}=\widehat{AOB}=120^0\)
Ta có độ dài cung \(AmB\) là: \({l_\overparen{AmB}}= \dfrac{\pi R.120}{180}= \dfrac{2\pi R}{3} = 2R.\dfrac{\pi }{3} \approx 2,09.R\)
Độ dài đường gấp khúc \(AOB\) là \(d.\)
\(\Rightarrow d = AO + OB = R + R = 2R.\)
Vậy \({l_\overparen{AmB}}>d.\)
