Đề bài
Cho tam giác \(ABC\) vuông ở \(A\) và đường cao \(AH.\) Vẽ đường tròn tâm \(O\) đường kính \(AB.\) Biết \(BH = 2cm\) và \(HC = 6cm.\) Tính:
\(a)\) Diện tích hình tròn \((O).\)
\(b)\) Tổng diện tích hai hình viên phân \(AmH\) và \(BnH\) (ứng với các cung nhỏ).
\(c)\) Diện tích hình quạt tròn \(AOH\) (ứng với cung nhỏ \(AH\)).
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Trong tam giác vuông, bình phương một cạnh góc vuông bằng tích cạnh huyền với hình chiếu của cạnh góc vuông đó trên cạnh huyền.
+) Diện tích \(S\) của một hình tròn bán kính \(R\) được tính theo công thức: \(S=\pi.R^2\)
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
Lời giải chi tiết
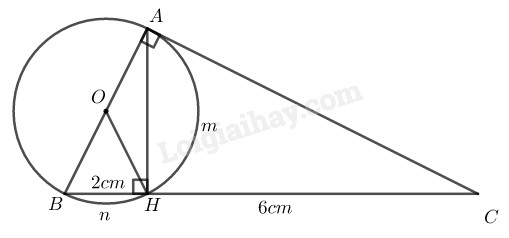
\(a)\) \(∆ABC\) có \(\widehat A = {90^0}\)
Theo hệ thức lượng trong tam giác vuông ta có:
\(A{B^2} = BH.BC \)\(\Rightarrow A{B^2} = 2.\left( {2 + 6} \right) = 16\)
Suy ra \(AB = 4\, (cm)\)
Diện tích hình tròn tâm \(O\) là:
\(S = \displaystyle \pi {\left( {{{AB} \over 2}} \right)^2} \)\(= \displaystyle \pi {\left( {{4 \over 2}} \right)^2} = 4\pi \) \( (cm^2)\)
\(b)\) Trong tam giác vuông \(ABC\) ta có:
\(A{H^2} = HB.HC = 2.6 = 12\)
Suy ra \(AH = 2\sqrt 3 \) \((cm)\)
\(S_{\Delta AHB}= \displaystyle {1 \over 2}AH.BH \)\(= \displaystyle {1 \over 2}.2.2\sqrt 3 = 2\sqrt 3 \) \( (cm^2)\)
Tổng diện tích hai hình viên phân \(AmH\) và \(BnH\) bằng diện tích nửa hình tròn tâm \(O\) trừ diện tích \(∆AHB\) nên tổng diện tích hai hình viên phân là:
\(S = 2\pi - 2\sqrt 3 = 2\left( {\pi - \sqrt 3 } \right)\) \( (cm^2)\)
\(c)\) \(∆BOH\) có \(OB = OH = BH = 2 cm\)
\( \Rightarrow \Delta BOH\) đều
\( \Rightarrow \widehat B = {60^0}\)
\(\widehat B = \displaystyle {1 \over 2} sđ \overparen{AmH}\) (tính chất góc nội tiếp)
\( \Rightarrow sđ \overparen{AmH}\) \( = 2\widehat B = {120^0}\)
\(S_{qAOH}=\displaystyle {{\pi {{.2}^2}.120} \over {360}} = \displaystyle {{4\pi } \over 3}\) \( (cm^2)\)
soanvan.me
