Cho hình lập phương ABCD.A’B’C’D’ có cạnh 1. Gọi M, N, P lần lượt là trung điểm của các cạnh B’B, CD và A’D’.
LG a
Tính khoảng cách giữa cặp đường thẳng A’B, B’D và cặp đường thẳng PI, AC’ (I là tâm của đáy ABCD).
Lời giải chi tiết:
Ta chọn hệ trục Oxyz sao cho gốc toa độ là A, Tia Ox chứa AB, tia Oy chứa AD và tia Oz chứa AA’(h.103).
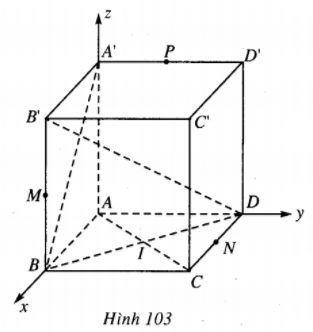
Khi đó
\(\eqalign{ & A = \left( {0;0;0} \right),B = \left( {1;0;0} \right) \cr & D = \left( {0;1;0} \right),A' = \left( {0;0;1} \right) \cr & C = \left( {1;1;0} \right),B' = \left( {1;0;1} \right) \cr & C' = \left( {1;1;1} \right),D' = \left( {0;1;1} \right). \cr} \)
Suy ra \(\overrightarrow {A'B} = \left( {1;0; - 1} \right)\)
\(\overrightarrow {B'D} = \left( { - 1; 1; - 1} \right)\)
\( \Rightarrow \left[ {\overrightarrow {A'B} ,\overrightarrow {B'D} } \right] = \left( {1;2;1} \right).\)
\(\overrightarrow {A'B'} = \left( {1;0;0} \right)\)
\(d\left( {A'B,B'D} \right) = {{\left| {\left[ {\overrightarrow {A'B} ,\overrightarrow {B'D} } \right].\overrightarrow {A'B'} } \right|} \over {\left| {\left[ {\overrightarrow {A'B} ,\overrightarrow {B'D} } \right]} \right|}} = {1 \over {\sqrt 6 }}.\)
Ta lại có :
\(\eqalign{ & \cr & P = \left( {0;{1 \over 2};1} \right),I = \left( {{1 \over 2};{1 \over 2};0} \right),\cr&\overrightarrow {IP} = \left( { - {1 \over 2};0;1} \right). \cr & \overrightarrow {AC'} = \left( {1;1;1} \right),\overrightarrow {AP} = \left( {0;{1 \over 2};1} \right) \cr} \)
Suy ra \(d\left( {PI,AC'} \right) = {{\left| {\left[ {\overrightarrow {IP} ,\overrightarrow {AC'} } \right].\overrightarrow {AP} } \right|} \over {\left| {\left[ {\overrightarrow {IP} ,\overrightarrow {AC'} } \right]} \right|}} = {{\sqrt {14} } \over {28}}.\)
LG b
Tính góc giữa hai đường thẳng MP và C’N.
Tính góc giữa hai mặt phẳng (PAI) và (DCC’D’).
Lời giải chi tiết:
Ta có \(M = \left( {1;0;{1 \over 2}} \right),N = \left( {{1 \over 2};1;0} \right)\)
\(\eqalign{ & \Rightarrow \overrightarrow {MP} = \left( { - 1;{1 \over 2};{1 \over 2}} \right),\overrightarrow {NC'} = \left( {{1 \over 2};0;1} \right) \cr & \Rightarrow \overrightarrow {MP} .\overrightarrow {NC'} = 0 \Rightarrow MP \bot NC'. \cr} \)
Mặt phẳng (PIA) có vectơ pháp tuyến: \(\overrightarrow n = \left[ {\overrightarrow {AP} ,\overrightarrow {AI} } \right] = \left( { - {1 \over 2};{1 \over 2}; - {1 \over 4}} \right).\)
Mặt phẳng (DCC’D’) có vectơ pháp tuyến là \(\overrightarrow {AD} = \left( {0;1;0} \right).\)
Gọi \(\varphi \) là góc giữa hai mặt phẳng trên thì
\(\cos \varphi = {{\left| {\overrightarrow n .\overrightarrow {AD} } \right|} \over {\left| {\overrightarrow n } \right|.\left| {\overrightarrow {AD} } \right|}} = {2 \over 3}.\)
soanvan.me
