Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng (ABCD) và SA=2a. Gọi M, N lần lượt là trung điểm của các cạnh SA, SD.
LG a
Tính khoảng cách từ đỉnh A tới mặt phẳng (BCM) và khoảng cách giữa hai đường thẳng SB, CN.
Lời giải chi tiết:
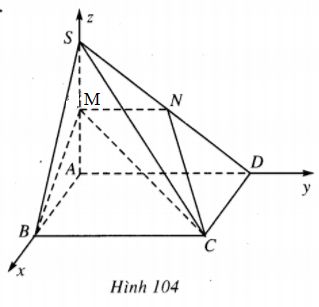
Chọn hệ trục Oxyz sao cho gốc O là điểm A, tia Ox chứa AB, tia Oy chứa AD và tia Oz chứa SA (h. 104).
Khi đó
\(\eqalign{ & A = \left( {0;0;0} \right),B = \left( {a;0;0} \right), \cr & C = \left( {a;a;0} \right),D = \left( {0;a;0} \right), \cr & S = \left( {0;0;2a} \right),M\left( {0;0;a} \right), \cr & N = \left( {0;{a \over 2};a} \right). \cr} \)
\(\overrightarrow {BC} = \left( {0;a;0} \right),\)
\(\overrightarrow {BM} = \left( { - a;0;a} \right)\)
\( \Rightarrow \left[ {\overrightarrow {BC} ,\overrightarrow {BM} } \right] = \left( {\left| {\matrix{ a & 0 \cr 0 & a \cr } } \right|;\left| {\matrix{ 0 & 0 \cr a & { - a} \cr } } \right|;\left| {\matrix{ 0 & a \cr { - a} & 0 \cr } } \right|} \right)\)
\(= \left( {{a^2};0;{a^2}} \right).\)
Do đó, mặt phẳng (BCM) có vectơ pháp tuyến là (1; 0; 1), suy ra phương trình mặt phẳng (BCM) là:
\(1\left( {x - a} \right) + 1\left( {z - 0} \right) = 0 \Leftrightarrow x + z -a= 0.\)
Vậy khoảng cách từ A đến mp(BCM)
\(d\left( {A,\left( {BCM} \right)} \right) = {{\left| { - a} \right|} \over {\sqrt {{1^2} + {1^2}} }} = {a \over {\sqrt 2 }}.\)
Ta lại có: \(\overrightarrow {BS} = \left( { - a;0;2a} \right),\overrightarrow {CN} = \left( { - a; - {a \over 2};a} \right),\)
\(\overrightarrow {SC} = \left( {a;a; - 2a} \right).\)
Suy ra
\(\left[ {\overrightarrow {BS} ,\overrightarrow {CN} } \right] \)
\(= \left( {\left| {\matrix{ 0 & {2a} \cr { - {a \over 2}} & a \cr } } \right|;\left| {\matrix{ {2a} & { - a} \cr a & { - a} \cr } } \right|;\left| {\matrix{ { - a} & 0 \cr { - a} & { - {a \over 2}} \cr } } \right|} \right) \)
\(= \left( {{a^2}; - {a^2};{{{a^2}} \over 2}} \right)\)
\( \Rightarrow \left[ {\overrightarrow {BS} ,\overrightarrow {CN} } \right].\overrightarrow {SC} = {a^3} - {a^3} - {a^3} = - {a^3}.\)
Vậy khoảng cách giữa hai đường thẳng SB và CN là
\(d\left( {SB,CN} \right) = {{\left| {\left[ {\overrightarrow {BS} ,\overrightarrow {CN} } \right].\overrightarrow {CN} } \right|} \over {\left| {\left[ {\overrightarrow {BS} ,\overrightarrow {CN} } \right]} \right|}} \)
\(= {{\left| { - {a^3}} \right|} \over {\sqrt {{a^4} + {a^4} + {{{a^4}} \over 4}} }} = {{{a^3}} \over {{{3{a^2}} \over 2}}} = {{2a} \over 3}.\)
LG b
Tính cosin của góc giữa hai mặt phẳng (SCD) và (SBC).
Lời giải chi tiết:
Vì \(\left[ {\overrightarrow {SC} ,\overrightarrow {SD} } \right] = \left( {0;2{a^2};{a^2}} \right)\) nên mp(SCD) có vectơ pháp tuyến \(\overrightarrow n = \left( {0;2;1} \right).\)
Vì \(\left[ {\overrightarrow {SB} ,\overrightarrow {SC} } \right] = \left( {2{a^2};0;{a^2}} \right)\) nên mp(SBC) có vectơ pháp tuyến \(\overrightarrow {n'} = \left( {2;0;1} \right).\)
Gọi \(\varphi \) là góc giữa hai mặt phẳng (SCD) và (SBC), ta có
\(\cos \varphi = {{\left| {\overrightarrow n .\overrightarrow {n'} } \right|} \over {\left| {\overrightarrow n } \right|\left| {\overrightarrow {n'} } \right|}} = {{\left| { - 1} \right|} \over {\sqrt 5 .\sqrt 5 }} = {1 \over 5}.\)
LG c
Tính tỉ số thể tích giữa hai phần của hình chóp S.ABCD chia bởi mặt phẳng (BCM).
Lời giải chi tiết:
\({V_{S.ABCD}} = {1 \over 3}{a^2}.2a = {2 \over 3}{a^3}.\)
Vì M là trung điểm của SA suy ra \(d\left( {S,\left( {BCM} \right)} \right) = d\left( {A,\left( {BCM} \right)} \right) = {a \over {\sqrt 2 }}.\)
Hình chóp S.ABCD bị mp(BCM) chia làm 2 phần, trong đó có một phần là hình chóp S.BCNM. Hình chóp này có đường cao bằng \(d\left( {S,\left( {BCM} \right)} \right) = {a \over {\sqrt 2 }}\) và đáy là hình thang BCNM có diện tích bằng \({1 \over 2}\left( {a + {a \over 2}} \right)a\sqrt 2 = {{3\sqrt 2 {a^2}} \over 4}.\)
Suy ra: \({V_{S.BCNM}} = {1 \over 3}.{{3\sqrt 2 {a^2}} \over 4}.{a \over {\sqrt 2 }} = {{{a^3}} \over 4}.\)
Vậy tỉ số thể tích giữa hai phần của hình chóp S.ABCD chia bởi mp(BCM) là: \({{{{{a^3}} \over 4}} \over {{{2{a^3}} \over 3} - {{{a^3}} \over 4}}} = {3 \over 5}.\)
soanvan.me
