Đề bài
Cho hình thang cân ABCD có đáy lớn AB = 15 cm, đáy nhỏ CD = 5 cm và góc A bằng \({60^o}\).
a) Tính cạnh BC.
b) Gọi M, N lần lượt là trung điểm của AB và CD. Tính MN.
Phương pháp giải - Xem chi tiết
Kẻ DE và CF vuông góc với AB (E,F thuộc AB) tạo thành hình chữ nhật CDEF từ đó tính được BF. Sử dụng các hệ thức lượng giác để tính được BC và MN.
Lời giải chi tiết
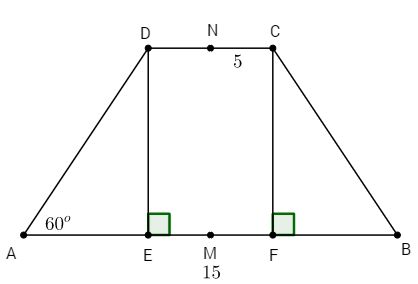
a) Tính cạnh BC.
Kẻ DE và CF vuông góc với AB (E,F thuộc AB) tạo thành hình chữ nhật CDEF có CD = 5 cm.
\( \Rightarrow \) CD = EF = 5 cm
Ta có: \(\Delta \)ADE = \(\Delta \)BCF (ch-gn) \( \Rightarrow \) AE = BF
Ta có: AB = AE + EF + BF hay 15 = BF + 5 + BF\( \Rightarrow \) BF = 5 cm
Xét \(\Delta \)BCF vuông tại F, ta có:
\(\cos \left( {\widehat B} \right) = \dfrac{{BF}}{{BC}}\)
\(\Rightarrow BC = \dfrac{{BF}}{{\cos \left( {\widehat B} \right)}} = \dfrac{5}{{\cos {{60}^o}}} = 10\)(cm)
b) Gọi M, N lần lượt là trung điểm của AB và CD. Tính MN.
Xét \(\Delta \) BCF vuông tại F, ta có:
\(\sin \left( {\widehat B} \right) = \dfrac{{CF}}{{BC}} \)
\(\Rightarrow CF = BC.\sin \left( {\widehat B} \right) = 10.\sin {60^o} \)\(\,= 5\sqrt 3 \) (cm)
Vì CDEF là hình chữ nhật nên DE = CF mà M, N lần lượt là trung điểm của AB và CD
\( \Rightarrow MN = DE = CF = 5\sqrt 3 \) cm
soanvan.me
