Đề bài
Hãy tìm độ dài cạnh đáy của một tam giác cân, nếu đường cao kẻ xuống đáy có độ dài là 5 và đường cao kẻ xuống cạnh bên có độ dài là 6.
Phương pháp giải - Xem chi tiết
Áp dụng tính chất về cạnh và đường cao của tam giác cân.
Vận dụng định lí Py-ta-go vào các tam giác vuông.
Lời giải chi tiết
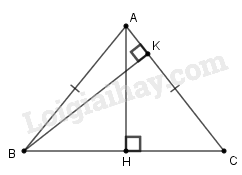
Giả sử \(∆ABC\) cân tại \(A\) có \(AH \bot BC,\)\(AH = 5,BK \bot AC,BK = 6.\)
Vì AH là đường cao của tam giác ABC cân tại A nên AH cũng là đường trung tuyến. Suy ra \(HB = HC = \displaystyle {1 \over 2}BC\) (tính chất tam giác cân)
\(\eqalign{
& {S_{ABC}} = \displaystyle {1 \over 2}AH.BC = {1 \over 2}BK.AC \cr
& = {1 \over 2}.5.BC = {1 \over 2}.6.AC \cr} \)
Suy ra: \(5BC = 6AC \Rightarrow BC = \displaystyle {6 \over 5}AC\,(1)\)
Áp dụng định lí Pi-ta-go vào tam giác vuông \(ACH\), ta có:
\(A{C^2} = A{H^2} + H{C^2} = {5^2} + \displaystyle {\left( {{{BC} \over 2}} \right)^2}\)\( = 25 + \displaystyle {{B{C^2}} \over 4}\,(2)\)
Từ (1) và (2) suy ra:
\(A{C^2} = 25 + {\displaystyle {{ {36A{C^2}} \over {25}}} \over 4}\)\( =\displaystyle {{2500} \over {100}} + {{36A{C^2}} \over {100}}\)
Suy ra:
\(100A{C^2} = 2500 + 36A{C^2}\)
\( \Leftrightarrow 64A{C^2} = 2500 \Leftrightarrow 8AC = 50\)\( \Rightarrow AC = 6,25\)
Vậy \(BC = \displaystyle {6 \over 5}.6,25 = 7,5.\)
soanvan.me
