Đề bài
Cho hình bình hành \(ABCD\) có \(\widehat A = 120^\circ \), \(AB = a,\) \(BC = b\). Các đường phân giác của bốn góc \(A, B, C, D\) cắt nhau tạo thành tứ giác \(MNPQ\). Tính diện tích tứ giác \(MNPQ\).
Phương pháp giải - Xem chi tiết
- Chứng minh \(MNPQ\) là hình chữ nhật.
- Áp dụng các tỉ số lượng giác để tính độ dài cạnh của hình chữ nhật.
- Tìm diện tích hình chữ nhật đó.
Lời giải chi tiết
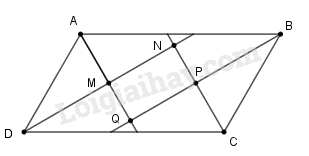
Vì ABCD là hình thoi nên \(\widehat {DCB} = \widehat {DAB} = {120^0},\) \(\widehat {ABC} = \widehat {ADC} = {180^0} - \widehat {BAD} \)\(= {180^0} - {120^0} = {60^0}\)
Từ giả thiết suy ra:
\(\widehat {ADM} = \widehat {MAB} = \widehat {ABP} \)\(= \widehat {CBP} = \dfrac{{{{60}^0}}}{2} = {30^0}\) (tính chất tia phân giác)
\(\widehat {DAM} = \widehat {BAM} = \widehat {DCP} \)\(= \widehat {PCB} = \dfrac{{{{120}^0}}}{2} = {60^0}\) (tính chất tia phân giác)
Tam giác ADM có \(\widehat {MDA} + \widehat {MAD} = {30^0} + {60^0} = {90^0}\) nên \(\widehat {AMD} = {180^0} - \left( {\widehat {MDA} + \widehat {MAD}} \right) \)\(= {180^0} - {90^0} = {90^0}\) \( \Rightarrow AM \bot DN \Rightarrow \widehat {NMQ} = {90^0}\)
Tam giác DNC có \(\widehat {NDC} + \widehat {NCD} = {30^0} + {60^0} = {90^0}\) nên \(\widehat {DNC} = {180^0} - \left( {\widehat {NDC} + \widehat {NCD}} \right) \)\(= {180^0} - {90^0} = {90^0}\) \( \Rightarrow \widehat {MNP} = {90^0}\)
Tam giác BPC có \(\widehat {PBC} + \widehat {PCB} = {30^0} + {60^0} = {90^0}\) nên \(\widehat {BPC} = {180^0} - \left( {\widehat {PBC} + \widehat {PCB}} \right) \)\(= {180^0} - {90^0} = {90^0}\) \( \Rightarrow BP \bot CN \Rightarrow \widehat {NPQ} = {90^0}\)
Từ đó suy ra, tứ giác \(MNPQ\) có \(3\) góc vuông nên \(MNPQ\) là hình chữ nhật.
Trong tam giác vuông ADM có \(DM = AD\sin \widehat {DAM} = b\sin 60^\circ\)\( = \displaystyle {{b\sqrt 3 } \over 2}.\)
Trong tam giác vuông \(DCN\) ( \(N\) là giao của đường phân giác góc \(D\) và đường phân giác góc \(C\)) có \(DN = DC\sin \widehat {DCN}{\rm{ = a\sin60}}^\circ {\rm{ = }}\)\(\displaystyle {{a\sqrt 3 } \over 2}.\)
Vậy \( \displaystyle MN = DN - DM = (a - b){{\sqrt 3 } \over 2}.\)
Trong tam giác vuông \(DCN\) có \( \displaystyle CN = DC\cos \widehat {DCN}= CD\cos 60^\circ = {a \over 2}.\) Trong tam giác vuông \(BCP\) ( \(P\) là giao của đường phân giác góc \(C\) với đường phân giác góc \(B\)) có \(CP =CB.\cos\widehat {PCB}=CB\cos 60^\circ = \displaystyle {b \over 2}.\)
Vậy: \(NP = CN - CP = \displaystyle {{a - b} \over 2}.\)
Suy ra diện tích hình chữ nhật \(MNPQ\) là
\(MN .NP = {(a - b)^2}\displaystyle {{\sqrt 3 } \over 4}\)
soanvan.me
