Đề bài
Cho hình thang \(ABCD\) có hai cạnh bên là \(AD\) và \(BC\) bằng nhau, đường chéo \(AC\) vuông góc với cạnh bên \(BC\). Biết \(AD = 5a\), \(AC = 12a.\)
a) Tính \(\displaystyle {{\sin B + c{\rm{osB}}} \over {\sin B - c{\rm{osB}}}}.\)
b) Tính chiều cao của hình thang \(ABCD\).
Phương pháp giải - Xem chi tiết
a) Áp dụng định lí Py-ta-go và tỉ số lượng giác.
b) Chiều cao hình thang ABCD bằng chiều cao tam giác ABC, áp dụng tỉ số lượng giác, tìm chiều cao của tam giác ABC.
Lời giải chi tiết
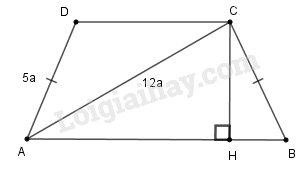
a) Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
\(A{B^2} = B{C^2} + A{C^2} = {(5a)^2} + {(12a)^2}\)\( = 169{a^2}\)
Suy ra: \(AB = \sqrt {169{a^2}} = 13a\)
Xét tam giác vuông ABC, theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:
\(\sin \widehat B = \displaystyle {{AC} \over {AB}} = {{12a} \over {13a}} = {{12} \over {13}}\)
\(\cos \widehat B = \displaystyle {{BC} \over {AB}} = {{5a} \over {13a}} = {5 \over {13}}\)
Suy ra:
\(\displaystyle {{\sin \widehat B + \cos \widehat B} \over {\sin \widehat B - \cos \widehat B}} = \displaystyle {\displaystyle {{{12} \over {13}} + {5 \over {13}}} \over {\displaystyle {{12} \over {13}} - {5 \over {13}}}}\)\( = \displaystyle {\displaystyle {{{17} \over {13}}} \over {\displaystyle {7 \over {13}}}} = {{17} \over {13}}.{{13} \over 7} = {{17} \over 7}\)
b) Kẻ \(CH \bot AB\)
Trong tam giác vuông \(BCH\), ta có:
\(CH = CB.\sin \widehat B = 5a.\displaystyle {{12} \over {13}} = {{60a} \over {13}}\)
soanvan.me
