Đề bài
Cho phép vị tự V có tâm O tỉ số k và phép vị tự V’ có tâm O’ tỉ số k’, biết rằng O, O’ là hai điểm phân biệt và kk’ = 1. Chứng minh rằng hợp thành của V và V’ là một phép tịnh tiến.
Lời giải chi tiết
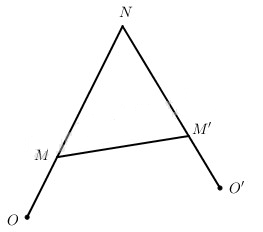
Lấy điểm M tùy ý và giả sử V biến điểm M thành điểm N và V’ biến điểm N thành điểm M’.
Khi đó ta có:
\(\overrightarrow {ON} = k\overrightarrow {OM} \) và \(\overrightarrow {O'M'} = k'\overrightarrow {O'N} \). (chú ý rằng kk’ = 1)
Suy ra
\(\eqalign{ & \overrightarrow {OO'} = \overrightarrow {OM} + \overrightarrow {MM'} + \overrightarrow {M'O'} \cr & = {1 \over k}\overrightarrow {ON} + \overrightarrow {MM'} - k'\overrightarrow {O'N} \cr & = \overrightarrow {MM'} + {1 \over k}\left( {\overrightarrow {ON} + \overrightarrow {NO'} } \right) \cr & = \overrightarrow {MM'} + {1 \over k}\overrightarrow {OO'} \cr} \)
Như vậy, ta có \(\overrightarrow {MM'} = \left( {1 - k} \right)\overrightarrow {OO'} \) (*)
Vì phéo hợp thành của V và V’ biến M thành M’ nên từ (*) ta suy ra phép hợp thành đó là phép tịnh tiến theo vectơ \(\left( {1 - k'} \right)\overrightarrow {OO'} \).
soanvan.me
