Đề bài
Cho tứ diện SABC, hai mặt phẳng (SAB) và (SBC) vuông góc với nhau và có SA vuông góc với mp(ABC), \(SB = a\sqrt 2 ,\widehat {B{\rm{S}}C} = {45^0},\widehat {ASB} = \alpha \).
a) Chứng minh rằng BC vuông góc với SB. Tìm điểm cách đều các điểm S, A, B, C.
b) Xác định α để hai mặt phẳng (SCA) và (SCB) tạo với nhau góc 60°.
Lời giải chi tiết
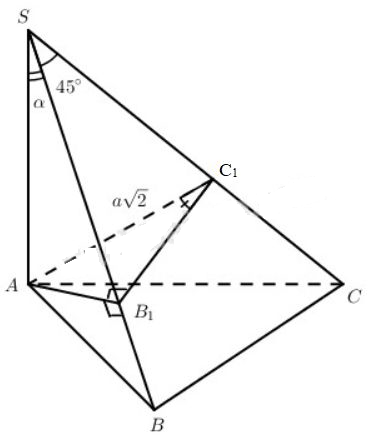
a) Vì
\(\eqalign{ & \left( {ABC} \right) \bot \left( {SAB} \right) \cr & \left( {SBC} \right) \bot \left( {SAB} \right) \cr} \)
mà \(BC = \left( {ABC} \right) \cap \left( {SBC} \right)\) nên \(BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\).
Như vậy, tứ diện SABC có \(\widehat {SAC} = {90^0}\) và \(\widehat {SBC} = {90^0}\) nên điểm cách đều S, A, B, C là trung điểm của SC.
Chú ý. Có thể chứng minh \(BC \bot SB\) như sau:
Kẻ \(A{B_1} \bot SB\) do \(\left( {SAB} \right) \bot \left( {SBC} \right)\) nên \(A{B_1} \bot \left( {SBC} \right)\)
\( \Rightarrow A{B_1} \bot BC\)
mặt khác \(BC \bot SA\)
\(\eqalign{ & \Rightarrow BC \bot \left( {SAB} \right) \cr & \Rightarrow BC \bot SB \cr} \)
b) Kẻ \(A{B_1} \bot SB,A{C_1} \bot SC\), dễ chứng minh được
\(A{B_1} \bot \left( {SBC} \right)\) và \(\left( {A{B_1}{C_1}} \right) \bot SC\).
Từ đó \(\widehat {A{C_1}{B_1}}\) là góc giữa hai mặt phẳng (SCA) và (SCB).
Xét ∆AB1C1 ta có \(A{B_1} = {B_1}{C_1}\tan {60^0}\)
mà \(A{B_1} = S{B_1}\tan \alpha ,{B_1}{C_1} = S{B_1}\sin {45^0}\).
Vậy hai mặt phẳng (SCA) và (SCB) tạo với nhau góc 60° khi và chỉ khi
\(S{B_1}\tan \alpha = S{B_1}.{{\sqrt 2 } \over 2}.\sqrt 3 \Leftrightarrow \tan \alpha = {{\sqrt 6 } \over 2}\).
Hệ thức này xác định α.
soanvan.me
