Đề bài
Cho hình chóp S.ABCD có đáy là hình bình hành. Một mặt phẳng (P) cắt các cạnh bên SA, SB, SC, SD lần lượt tại A’, B’, C’, D’. Chứng minh rằng tứ giác A’B’C’D’ là hình bình hành khi và chỉ khi mặt phẳng (P) song song với mp(ABCD).
Lời giải chi tiết
(h.97)
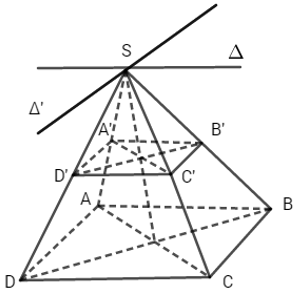
- Giả sử A’B’C’D’ là hình bình hành. Ta có:
A’B’ // C’D’
A’B’ \( \subset \) (SAB)
C’D’ \( \subset \) (SCD)
Suy ra giao tuyến \(\Delta \) của (SAB) và (SCD) song song với A’B’ và C’D’.
Mặt khác:
\(\left. \matrix{
AB//CD \hfill \cr
AB \subset \left( {SAB} \right) \hfill \cr
CD \subset \left( {SCD} \right) \hfill \cr} \right\} \Rightarrow \Delta //AB//CD\)
Vậy A’B’ // AB \( \Rightarrow \) A’B’ // (ABCD) (1)
Chứng minh tương tự, ta có
A’D’ // AD \( \Rightarrow \) A’D’ //(ABCD) (2)
Từ (1) và (2) suy ra (P) // (ABCD).
- Giả sử (P) // (ABCD).
Khi đó hai mặt phẳng (P) và (ABCD) bị mặt phẳng (SAB) cắt theo hai giao tuyến A’B’ và AB song song
Tương tự, ta có:
C’D’ // CD
B’C’ // BC
A’D’ // AD
Suy ra: A’B’ // C’D’ và B’C’ // A’D’
Vậy tứ giác A’B’C’D’ là hình bình hành.
soanvan.me
