Đề bài
Cho tứ diện ABCD. Hai điểm M, N lần lượt thay đổi trên hai cạnh AB và CD. Tìm tập hợp trung điểm I của MN.
Lời giải chi tiết
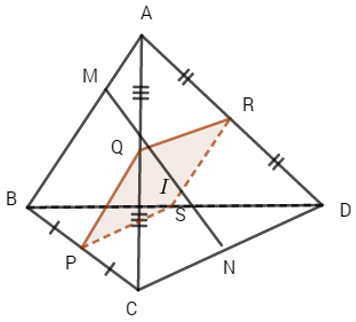
Phần thuận. Giả sử I là trung điểm của MN. Gọi P, Q, R, S lần lượt là trung điểm của BC, CA, AD và DB. Vì:
\({{PB} \over {IM}} = {{PC} \over {IN}} = {{BC} \over {MN}}\)
Nên BM, PI, CN cùng song song với một mặt phẳng, mặt phẳng này song song với AB và CD. Gọi \(\left( \alpha \right)\) là mặt phẳng qua P và song song với mặt phẳng đó thì rõ ràng \(I \in \left( \alpha \right)\). Mặt phẳng này cắt tứ diện ABCD theo thiết diện là hình bình hành PQRS. Vì M chỉ chạy trên đoạn AB, N chỉ di động trên CD nên điểm I luôn nằm trong tứ diện, tức là I luôn nằm trong hình bình hành PQRS.
Phần đảo. Lấy một điểm I nằm trong hình hình bình hành PQRS. Qua I có một đường thẳng cắt hai cạnh AB và CD tại M và N. Theo định lí Ta-lét thì I là trung điểm của MN.
Vậy tập hợp các điểm I là hình bình hành PQRS (cùng với các điểm trong của nó).
soanvan.me
