Đề bài
Cho lăng trụ tam giác ABC.A’B’C’. Trên đường thẳng BA lấy một điểm M sao cho A nằm giữa B và M, \(MA = {1 \over 2}AB\)
a) Xác định thiết diện của hình lăng trụ khi cắt bởi mặt phẳng (P) qua M, B’ và trung điểm E của AC.
b) Tính tỉ số \({{BD} \over {CD}}\left( {D = BC \cap mp\left( {MB'E} \right)} \right)\).
Lời giải chi tiết
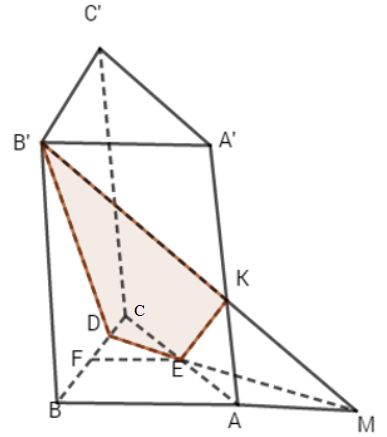
a) Trong mp(ABB’A’) nối M với B’ cắt AA’ tại K.
Trong mp(ABC) nối M với E cắt CB tại D.
Thiết diện là tứ giác DEKB’.
b) Kẻ EF // AB \(\left( {F \in CB} \right)\). Khi đó EF là đường trung bình của tam giác ABC và \({\rm{EF}} = {{AB} \over 2}\).
Xét tam giác DBM ta có:
\({{FD} \over {BD}} = {{EF} \over {BM}} = {1 \over 3}\)
Suy ra FD = \({1 \over 2}\)BF = FC, tức D là trung điểm FC.
Vậy \({{BD} \over {CD}} = 3\).
soanvan.me
