Đề bài
Cho hình chóp S.ABCD có đáy là hình thang \(\left( {AB//CD,\,AB > CD} \right).\) Gọi E là giao điểm của AD và BC; M là trung điểm của AB; G là trọng tâm của tam giác ECD.
a) Chứng minh rằng các điểm S, E, M, G cũng thuộc một mặt phẳng và mặt phẳng này cắt cả hai mặt phẳng (SAC) và (SBD) theo cùng một đường thẳng \(\Delta \).
b) Gọi \({C_1}\) và \({D_1}\) là hai điểm lần lượt thuộc các cạnh SC, SD sao cho \(A{D_1}\) và \(B{C_1}\) cắt nhau tại K. Chứng minh các điểm S, K, E thẳng hàng và giao điểm \({O_1}\) của \(A{C_1}\) với \(B{D_1}\) thuộc \(\Delta \).
Lời giải chi tiết
a) Gọi N là giao điểm của EM và CD. Do M là trung điểm của AB và AB // CD nên N cũng là trung điểm của CD; suy ra G thuộc EM, hay \(G \in mp\left( {SEM} \right),\) tức là các điểm S, E, M , G thuộc mp(SEM).
Gọi O là giao điểm của AC và BD thì đường thẳng MN đi qua O. Vậy ba mặt phẳng (SEM), (SAC) và (SBD) đều có chung hai điểm S và O nên SO chính là giao tuyến chung \(\Delta \) của ba mặt phẳng trên.
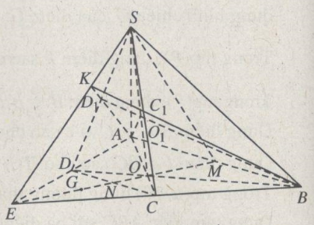
b) Vì K thuộc \(A{D_1}\) và \(B{C_1}\) nên tương ứng K thuộc mp(SAD) và mp(SBC). Do đó K nằm trên giao tuyến SE của hai mặt phẳng (SAD) và (SBC). Vậy ba điểm S, E, K thẳng hàng.
Điểm \({O_1}\) nằm trên \(A{C_1}\) và \(B{D_1}\) nên \({O_1}\) phải thuộc (SAC) và (SBD) (do \(A{C_1} \subset \left( {SAC} \right),\,B{D_1} \subset \left( {SBD} \right)\)). Từ đó, suy ra \({O_1}\) phải thuộc giao tuyến \(\Delta \) của hai mặt phẳng (SAC) và (SBD).
soanvan.me
