Đề bài
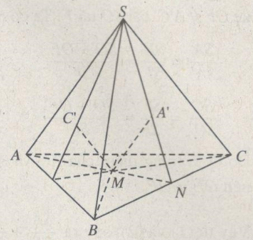
Cho hình chóp S.ABC và một điểm M nằm trong tam giác ABC. Các đường thẳng qua M lần lượt song song với các đường thẳng SA, SB, SC cắt các mặt phẳng (SBC), (SCA), (SAB) tại A’, B’, C’.
a) Gọi N là giao điểm của SA’ với BC. Chứng minh rằng các điểm A, M, N thẳng hàng và từ đó suy ra cách dựng điểm A’.
b) Chứng minh rằng \({{{S_{MBC}}} \over {{S_{ABC}}}} = {{MA'} \over {SA}};\)
c) Chứng minh rằng \({{MA'} \over {SA}} + {{MB'} \over {SB}} + {{MC'} \over {SC}} = 1.\)
Lời giải chi tiết
a) Vì A’M//SA nên có mp(MA’,SA). Mặt phẳng này và mặt phẳng (ABC) có ba điểm chung A, M, N. Do đó ba điểm A, M, N phải nằm trên giao tuyến của hai mặt phẳng nói trên. Vậy ba điểm đó phải thẳng hàng.
Kéo dài AM cắt BC tại N. Trong mp(SAN) kẻ MA’ song song với SA cắt SN tại A’. Điểm A’ là điểm cần tìm.
Tương tự xác định được các điểm B’, C’.
b) Dễ thấy \({{{S_{MBC}}} \over {{S_{ABC}}}} = {{MN} \over {AN}}\)
Mà \({{MN} \over {AN}} = {{MA'} \over {SA}}.\)
Vậy \({{{S_{MBC}}} \over {{S_{ABC}}}} = {{MA'} \over {SA}}.\)
c) Chứng minh tương tự như câu b), ta có:
\({{{S_{MCA}}} \over {{S_{ABC}}}} = {{MB'} \over {SB}},\,{{{S_{MAB}}} \over {{S_{ABC}}}} = {{MC'} \over {SC}}.\)
Vậy \({{MA'} \over {SA}} + {{MB'} \over {SB}} + {{MC'} \over {SC}} = {{{S_{MBC}} + {S_{MCA}} + {S_{MAB}}} \over {{S_{ABC}}}}\)
\( = {{{S_{ABC}}} \over {{S_{ABC}}}} = 1.\)
soanvan.me
