Đề bài
Cho tứ diện ABCD. Một mặt phẳng \(\left( \alpha \right)\) song song với cả AC và BD cắt các cạnh AB, BC, CD, DA lần lượt tại các điểm P, Q, R, S.
a) Chứng minh rằng tứ giác PQRS là hình bình hành.
b) Xác định vị trí của điểm P trên cạnh AB để tứ giác PQRS là hình thoi.
Lời giải chi tiết
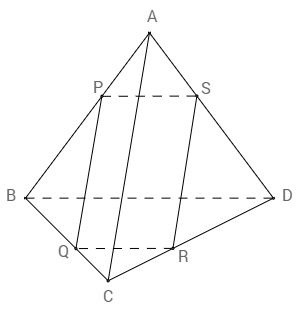
a)
\(\left. \matrix{
AC//\alpha \hfill \cr
AC \subset \left( {ABC} \right) \hfill \cr
(\alpha ) \cap (ABC) = PQ \hfill \cr} \right\} \Rightarrow PQ//AC\)
\(\left. \matrix{
AC//\alpha \hfill \cr
AC \subset \left( {ACD} \right) \hfill \cr
(\alpha ) \cap (ACD) = RS \hfill \cr} \right\} \Rightarrow RS//AC\)
Từ trên, suy ra: PQ // RS (//AC) (1)
Chứng minh tương tự, ta có:
PS // QR (//BD) (2)
Từ (1) và (2) suy ra tứ giác PQRS là hình bình hành.
b) Vì \(PS//BD \Rightarrow {{PS} \over {BD}} = {{PA} \over {AB}}\)
Nên \(PS = {{BD} \over {AB}}.PA.\) (3)
Vì \(PQ//AC \Rightarrow {{PQ} \over {AC}} = {{PB} \over {AB}}\)
Nên \(PQ = {{AC} \over {AB}}.PB.\) (4)
Tứ giác PQRS là hình thoi khi và chỉ khi PS = PQ
\(\eqalign{
& \Leftrightarrow BD.PA = AC.PB \cr
& \Leftrightarrow {{PA} \over {PB}} = {{AC} \over {BD}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(5) \cr} \)
Tứ giác PQRS là hình thoi khi và chỉ khi \(mp\left( \alpha \right)\) qua điểm P (được xác định bởi (5)) đồng thời song song với cả AC và BD.
soanvan.me
