Câu hỏi 1 :
Một vật dao động điều hòa theo phương trình \(x = 5cos\left( {\pi t} \right)cm\). Gia tốc cực đại của vật bằng:
- A
\(5cm/{s^2}\)
- B
\(5\pi cm/{s^2}\)
- C
\(5{\pi ^2}cm/{s^2}\)
- D
\(25{\pi ^2}cm/{s^2}\)
Đáp án: C
Phương pháp giải:
Vận dụng biểu thức xác định gia tốc cực đại: \({a_{max}} = {\omega ^2}A\)
Lời giải chi tiết:
Gia tốc cực đại: \({a_{max}} = {\omega ^2}A = {\pi ^2}.5 = 5{\pi ^2}\left( {cm/{s^2}} \right)\)
Câu hỏi 2 :
Một con lắc đơn có chiều dài \(l\), dao động điều hòa tại nơi có gia tốc trọng trường \(g\). Tần số dao động của con lắc được xác định bởi biểu thức:
- A
\(f = 2\pi \sqrt {\frac{g}{l}} \)
- B
\(f = 2\pi \sqrt {\frac{l}{g}} \)
- C
\(f = \frac{1}{{2\pi }}\sqrt {\frac{g}{l}} \)
- D
\(f = \frac{1}{{2\pi }}\sqrt {\frac{l}{g}} \)
Đáp án: C
Lời giải chi tiết:
Tần số dao động của con lắc đơn: \(f = \frac{1}{{2\pi }}\sqrt {\frac{g}{l}} \)
Câu hỏi 3 :
Tại một nơi xác định, chu kì dao động điều hòa của con lắc đơn tỉ lệ nghịch với:
- A
Căn bậc hai chiều dài con lắc
- B
Chiều dài con lắc
- C
Căn bậc hai gia tốc trọng trường
- D
Gia tốc trọng trường
Đáp án: C
Phương pháp giải:
Vận dụng biểu thức tính chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \)
Lời giải chi tiết:
Ta có chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \)
=> Chu kì dao động của con lăc đơn tỉ lệ thuận với căn bậc 2 chiều dài con lắc và tỉ lệ nghịch với căn bậc hai gia tốc trọng trường
Câu hỏi 4 :
Một vật dao động điều hòa theo phương trình \(x = Acos(ωt + φ)\) \((ω > 0)\). Tần số góc của dao động là:
- A
A
- B
ω
- C
φ
- D
x
Đáp án: B
Phương pháp giải:
Đọc phương trình dao động điều hòa
Lời giải chi tiết:
Phương trình dao động điều hòa:\(x = Acos(ωt + φ)\)
Trong đó, tần số góc của dao động là \(\omega\)
Câu hỏi 5 :
Gốc thời gian được chọn vào lúc nào nếu phương trình dao động điều hòa có dạng \(x = A\cos \left( {\omega t + {\pi \over 2}} \right)cm\)?
- A Lúc chất điểm qua vị trí cân bằng theo chiều dương qui ước.
- B Lúc chất điểm có li độ x = - A.
- C Lúc chất điểm có li độ x = + A.
- D Lúc chất điểm qua vị trí cân bằng theo chiều âm qui ước.
Đáp án: D
Phương pháp giải:
Sử dụng đường tròn lượng giác
Lời giải chi tiết:
Phương trình dao động là: \(x = A\cos \left( {\omega t + {\pi \over 2}} \right)cm\)
Pha ban đầu là $π/2$.
Biểu diễn trên đường tròn lượng giác ta có:
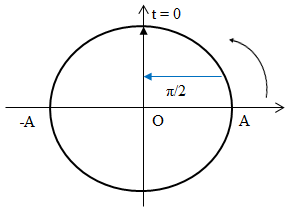=> Gốc thời gian được chọn là lúc chất điểm đi qua VTCB theo chiều âm quy ước.
Câu hỏi 6 :
Một con lắc lò xo dao động không ma sát trên một mặt phẳng ngang. Phát biểu nào sau đây sai:
- A
Dao động của con lắc là dao động tuần hoàn.
- B
Dao động của con lắc là dao động điều hòa.
- C
Thời gian thực hiện một dao động càng lớn khi biên độ càng lớn.
- D
Số dao động thực hiện được trong 1s tỉ lệ thuận với căn bậc hai của độ cứng k.
Đáp án: C
Lời giải chi tiết:
A, B - đúng vì dao động của con lắc lò xo là dao động điều hòa mà dao động điều hòa là trường hợp riêng của dao động tuần hoàn
D - đúng vì: số dao động vật thực hiện trong 1s là tần số
\(f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} \) (tỉ lệ thuận với căn bậc 2 của k)
C - sai vì chu kì dao động không phụ thuộc vào biên độ
Câu hỏi 7 :
Một con lắc đơn gồm vật nặng có khối lượng m, dây treo dài l. Kéo vật ra khỏi vị trí cân bằng một góc α0 rồi thả cho vật dao động. Biểu thức xác định lực căng dây tại vị trí α bất kì là:
- A
\(T = mg(3c{\rm{os}}{\alpha _0}{\rm{ - 2cos}}\alpha )\)
- B
\(T = mg(3c{\rm{os}}\alpha {\rm{ - 2cos}}{\alpha _0})\)
- C
\(T = mg(c{\rm{os}}{\alpha _0}{\rm{ - cos}}\alpha )\)
- D
\(T = mg(c{\rm{os}}\alpha {\rm{ - cos}}{\alpha _0})\)
Đáp án: B
Lời giải chi tiết:
Biểu thức xác định lực căng dây tại vị trí α bất kì: \(T = mg(3c{\rm{os}}\alpha {\rm{ - 2cos}}{\alpha _0})\)
Câu hỏi 8 :
Một vật dao động điều hòa với chu kỳ \(T\) và biên độ \(A\). Khoảng thời gian ngắn nhất vật đi từ vị trí có động năng bằng thế năng đến vị trí có động năng bằng 3 lần thế năng là?
- A
\(\dfrac{T}{3}\)
- B
\(\dfrac{T}{4}\)
- C
\(\dfrac{T}{6}\)
- D
\(\dfrac{T}{{24}}\)
Đáp án: D
Phương pháp giải:
+ Áp dụng biểu thức xác định cơ năng: \({\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_{\rm{d}}}\)
+ Sử dụng vòng tròn lượng giác và biểu thức: \(\Delta \varphi = \omega \Delta t\)
Lời giải chi tiết:
Ta có:
+ Vị trí có động năng bằng thế năng:
\({{\rm{W}}_t} = {{\rm{W}}_{đ}} \to 2{{\rm{W}}_t} = {\rm{W}} \to {x_1} = \pm \dfrac{A}{{\sqrt 2 }}\)
+ Vị trí có động năng bằng 3 lần thế năng:
\({{\rm{W}}_d} = 3{{\rm{W}}_t} \to {{\rm{W}}_t} = \dfrac{{\rm{W}}}{4} \to {x_2} = \pm \dfrac{A}{2}\)
Xác định các vị trí trên vòng tròn lượng giác, ta được:
Câu hỏi 9 :
Một vật dao động điều hòa với biên độ $A = 8cm$ và $ω = π rad/s$. Tại thời điểm ban đầu vật qua vị trí có li độ \({x_0} = {\text{ }}4cm\) theo chiều âm. Phương trình dao động của vật là:
- A
\(x = 8cos\left( {\pi t - \frac{\pi }{3}} \right)\left( {cm} \right)\)
- B
\(x = 8cos\left( {\pi t - \frac{{2\pi }}{3}} \right)(cm)\)
- C
\(x = 8cos\left( {\pi t + \frac{\pi }{3}} \right)\left( {cm} \right)\)
- D
\(x = 8cos\left( {\pi t + \frac{{2\pi }}{3}} \right)\left( {cm} \right)\)
Đáp án: C
Phương pháp giải:
Xác định pha ban đầu: Tại $t=0$: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi \\{\rm{v = - A}}\omega {\rm{sin}}\varphi \end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\frac{{{x_0}}}{A}\\\sin \varphi = - \frac{v}{{A\omega }}\end{array} \right. \to \varphi = ?\)
Lời giải chi tiết:
Ta có A =8cm, ω = π rad/s
Tại t = 0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = 4\\{\rm{v = - A}}\omega {\rm{sin}}\varphi < 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\frac{{{x_0}}}{A} = \frac{4}{8} = \frac{1}{2}\\\sin \varphi > 0\end{array} \right. \to \varphi = \frac{\pi }{3}\)
=> x =8cos(πt +π/3)(cm)
Câu hỏi 10 :
Một vật có khối lượng $m = 200 (g)$, dao động điều hoà với phương trình $x=10cos(5\pi t)cm$ . Tại thời điểm $t=0,5(s)$ thì vật có động năng là:
- A
Wđ = 0,125 J
- B
Wđ = 0,25 J
- C
Wđ = 0,2 J
- D
Wđ = 0,1 J
Đáp án: B
Phương pháp giải:
+ Cách 1: Từ phương trình li độ, viết phương trình vận tốc, thay t vào phương trình vận tốc suy ra v
Áp dụng biểu thức tính động năng của con lắc lò xo: \(W = \frac{1}{2}m{v^2}\)
+ Cách 2: Thay t vào phương trình li độ, từ x dùng hệ thức độc lập A - x - v suy ra vận tốc: \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}\)
Áp dụng biểu thức tính động năng của con lắc lò xo: \(W = \frac{1}{2}m{v^2}\)
Lời giải chi tiết:
Cách 1:
Phương trình vận tốc của vật: v = x’(t) = -50psin(5pt) cm/s (1)
Tại t = 0,5s thay vào (1) => v = -50p
=> Động năng của vật:
\({{\text{W}}_d} = \frac{1}{2}m{v^2} = \frac{1}{2}.0,2.{(0,5\pi )^2} = 0,25J\)
Cách 2:
Thay t = 0,5s vào phương trình dao động, ta có: x = 0
=> vmax
=> Động năng của vật khi đó chính bằng cơ năng:
\({{\text{W}}_d} = \frac{1}{2}m{v^2} = \frac{1}{2}m{\omega ^2}{A^2} = \frac{1}{2}.0,2.{(5\pi .0,1)^2} = 0,25J\)
Câu hỏi 11 :
Một con lắc lò xo dao động điều hòa theo phương thẳng đứng với chu kì $0,4s$ và biên độ $8cm$. lấy $g = 10 m/s^2$ và \({\pi ^2} \approx 10\). Khoảng thời gian ngắn nhất giữa hai lần công suất tức thời của lực đàn hồi bằng $0$ là:
- A
$1/30s$
- B
$2/15s$
- C
$1/15s$
- D
$4/15s$
Đáp án: C
Phương pháp giải:
+ Áp dụng biểu thức tính độ dãn tại vị trí cân bằng của con lắc lò xo treo thẳng đứng: \(\Delta l = \dfrac{{mg}}{k}\)
+ Áp dụng biểu thức tính lực đàn hồi:
\({F_{dh}} = k(\Delta l + x)\)
+ Áp dụng biểu thức tính công suất tức thời: $P = |Fv|$
+ Sử dụng vòng tròn lượng giác và trục thời gian suy ra từ vòng tròn
Lời giải chi tiết:
Chọn chiều dương hướng xuống, ta có:
Độ dãn của lò xo tại vị trí cân bằng:
\(\Delta l = \dfrac{{mg}}{k} = \dfrac{{mg}}{{m{\omega ^2}}} = \dfrac{g}{{{{\left( {\dfrac{{2\pi }}{T}} \right)}^2}}} = \dfrac{{10}}{{{{\left( {\dfrac{{2\pi }}{{0,4}}} \right)}^2}}} = 0,04m = 4cm\)
Lực đàn hồi tại vị trí bất kì:
\({F_{dh}} = k(\Delta l + x)\)
Công suất tức thời: \(P = \left| {Fv} \right| = k\left| {(\Delta l + x)v} \right|\)
Ta có: P = 0 khi \(\left[ \begin{array}{l}x = - \Delta l = - 4cm\\v = 0 \to x = \pm A\end{array} \right.\)
Vẽ vòng tròn lượng giác, ta được:
Câu hỏi 12 :
Một con lắc đơn có chiều dài dây treo \(l = 1m\) và quả nặng có khối lượng \(m{\rm{ }} = {\rm{ }}400{\rm{ }}g\) mang điện tích \(q = {4.10^{ - 6}}C\). Lấy \(g = 10 = {\pi ^2}m/{s^2}\). Đặt con lắc vào vùng không gian có điện trường điều mà có phương trùng với phương của trọng lực thì chu kì dao động của con lắc là \(2,04{\rm{ }}s\). Xác định hướng và độ lớn của điện trường ?
- A
E = 0,25.105V/m; hướng xuống
- B
E = 0,51.105V/m; hướng xuống
- C
E = 0,25.105V/m; hướng lên
- D
E = 0,51.105V/m; hướng lên
Đáp án: D
Phương pháp giải:
+ Áp dụng công thức tính chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\dfrac{l}{g}} \)
+ Áp dụng bài toán con lắc đơn chịu thêm tác dụng của lực điện
Lời giải chi tiết:
Ta có:
+ Chu kì dao động của con lắc khi chưa tích điện: \(T = 2\pi \sqrt {\dfrac{l}{g}} = 2\pi \sqrt {\dfrac{1}{{10}}} = 1,987{\rm{s}}\)
+ Khi con lắc tích điện \(q{\rm{ }} > {\rm{ }}0\), ta có chu kì T’: \(T' = 2\pi \sqrt {\dfrac{l}{{g'}}} = 2,04s > T\)
=> g’ < g
=> Lực điện \(\overrightarrow {{F_d}} \)hướng lên.
Ta có: \(q{\rm{ }} > {\rm{ }}0\) =>\(\overrightarrow E \) hướng lên